![]() De ce qui précède, il résulte que le produit
scalaire de deux vecteurs kets normés tel que
De ce qui précède, il résulte que le produit
scalaire de deux vecteurs kets normés tel que
![]() possède une signification physique directe. Le carré de son
module évalue une probabilité de transition. C'est pour cette
raison que le produit scalaire lui-même s'appelle une
amplitude de probabilité de transition :
possède une signification physique directe. Le carré de son
module évalue une probabilité de transition. C'est pour cette
raison que le produit scalaire lui-même s'appelle une
amplitude de probabilité de transition :
![]() Tout se passe comme si la mesure avait provoqué une
transition de l'état
Tout se passe comme si la mesure avait provoqué une
transition de l'état ![]() vers l'état
vers l'état ![]() , notée
, notée
![]() . En ce sens, on peut dire que la mesure a provoqué une
perturbation de l'état. On notera qu'une telle perturbation n'a rien de
commun avec une perturbation d'origine expérimentale, due à une
défectuosité de cet appareillage (mesure non idéale).
. En ce sens, on peut dire que la mesure a provoqué une
perturbation de l'état. On notera qu'une telle perturbation n'a rien de
commun avec une perturbation d'origine expérimentale, due à une
défectuosité de cet appareillage (mesure non idéale).
![]() On remarque l'implication réciproque :
On remarque l'implication réciproque :
Puisque une mesure idéale classique prétend ne pas perturber ou modifier
l'état du système physique observé :
il en résulte que, en général, tout se passe comme si les états considérés par la physique classiqueII14 étaient tous orthogonaux entre eux.
![]() Quand tout ou partie des observables mesurées, par exemple
Quand tout ou partie des observables mesurées, par exemple
![]() , possède un spectre continu de valeurs propres
, possède un spectre continu de valeurs propres ![]() , l'état final
considéré ci-dessus est celui provoqué par la réduction du paquet d'ondes
et est donc de la forme :
, l'état final
considéré ci-dessus est celui provoqué par la réduction du paquet d'ondes
et est donc de la forme :
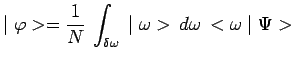 |
l'intervalle
![]() étant défini par la
précision expérimentale de la mesure et le facteur
étant défini par la
précision expérimentale de la mesure et le facteur ![]() étant choisi tel que
étant choisi tel que
![]() . Il en résulte
:
. Il en résulte
:
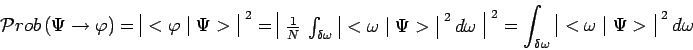 |
et si
![]() est infinitésimal, c'est-à-dire
est infinitésimal, c'est-à-dire
![]() :
:
Les résultats obtenus sont bien identiques à ceux obtenus par application immédiate du principe de décomposition spectrale.
En particulier si une particule est dans un état quelconque non localisé :
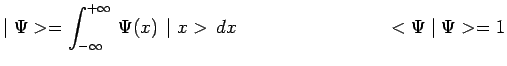 |
mesurer sa position, c'est lui en donner une, et si on trouve :
![]() c'est par exemple la mettre dans l'état :
c'est par exemple la mettre dans l'état :
 |
de telle sorte que :
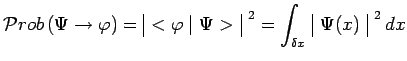 |
La fonction d'onde ![]() désigne donc bien une amplitude de densité de
probabilité de localisation de la particule.
désigne donc bien une amplitude de densité de
probabilité de localisation de la particule.