3) Sur un miroir

L'observation visuelle des rayons lumineux incidents et réfléchis parait alors indiquer que seule la partie centrale du miroir est utile à la réflexion. Cette suggestion semble encore renforcée par le modèle corpusculaire de la lumière, au moins sous sa première forme naïve, puisqu'un photon ne peut explorer que la région très limitée $\sigma$ de la surface du miroir sur laquelle il semble rebondir.

Si ce point de vue était exact, le phénomène de réflexion demeurerait inchangé si la surface du miroir était réduite à cette seule partie $\sigma$ puisqu'elle serait la seule utile. Or, on sait que la réflexion disparait alors, et qu'un nouveau phénomène apparait, étudié plus loin et appelé la diffraction.   On est donc amené à segmenter toute la surface du miroir en $n$ bandes $\sigma_1,~\sigma_2,~\ldots,~\sigma_n$ étroites de largeur $\varepsilon$ et parallèles à la fente lumineuse $S$ et perpendiculaires au plan de figure, de façon à préciser la contribution apportée au phénomène global de réflexion par chacune des portions du miroir.

Dès lors, on est amené à considérer que pour aller de la source $S$ au photo-multiplicateur récepteur $R$ , chaque photon peut être réfléchi sur l'une quelconque des $n$ bandes du miroir. Puisque le dispositif expérimental ne permet pas, par hypothèse, de discriminer ces diverses éventualités, en repérant avec quelle bande le photon incident a éventuellement interagi, les contributions de ces bandes s'ajoutent de façon cohérente, c'est-à-dire que ce sont les amplitudes de probabilité qui s'ajoutent et non pas les probabilités elles-mêmes. Quant à l'expression de ces amplitudes, nous utiliserons encore le modèle simple précédent de telle sorte que finalement :

$$\mathcal{P}(S\to R) = \begin{array}{\vert c\vert}\vec{Z}\\ \end{array}^{\,2} ~=~ \b... ...c\vert}\vec{Z_1}+\vec{Z_2}+\ldots+\vec{Z_n}\\ \end{array}^{\,2}$$

avec :

$$Z_i = A\,e^{i\,\varphi_0}~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{et}~~~~~~~~~~~~~~~~~~~~~~~~\varphi_i ~=~ 2\pi~\frac{\ell_i}{\lambda}$$

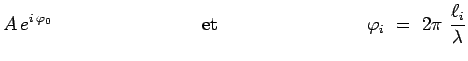et la construction graphique ci-après en résulte aussitôt, en choisissant arbitrairement la valeur initiale $\varphi_1$ des $\varphi_i$ . On notera toutefois que la valeur $\varphi_i$ associée à chaque élément $\sigma_i$ n'a de sens que si $\varepsilon \lesssim \lambda$ , de telle sorte que la valeur de $\varphi_i$ et donc de $\ell_i$ est à peu près la même pour tous les points de $\sigma_i$ .

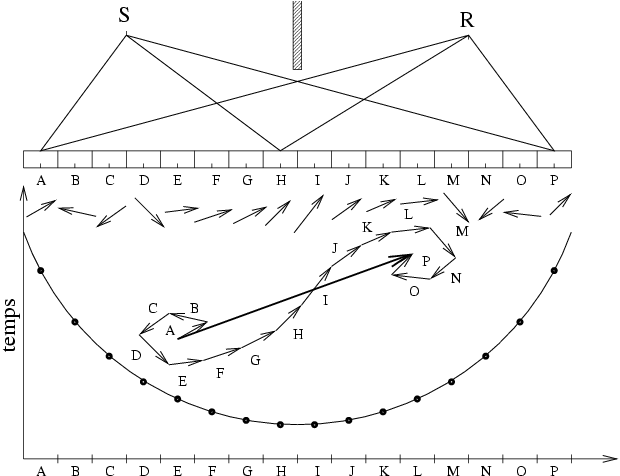
On constate que l'amplitude globale $Z$ fait essentiellement intervenir les contributions des éléments $\sigma_i$ voisins du point I de réflexion classique. C'est en effet au voisinage de I que la phase $\varphi$ varie peu et que les vecteurs $\vec{Z}_i$ ont des directions voisines. La raison en est qu'au point I la phase est stationnaire, en même temps que le chemin $\ell$ et la durée du trajet $t$ sont minimum comme l'indique par ailleurs le principe de Fermat. Les éléments $\sigma_i$ éloignés du point I contribuent très peu car les déphasages associés à leurs contributions font que celles-ci se détruisent mutuellement.