Réflexion et transmission de la lumière par la matière

Nous nous proposons d'illustrer ci-après les règles quantiques de sommation et de multiplication des amplitudes de probabilité de transition et de montrer comment le seul fonctionnement de ces règles, lestées toutefois par le contenu physique d'un modèle très simple, permet d'expliquer tout un ensemble de phénomènes physiques mettant en jeu la lumière et ses interactions avec la matière.

A cet effet, nous nous proposons de résumer les quatre conférences de Feynman qui ont été publiées dans l'excellent ouvrage intitulé ``Lumière et Matière''.

Dans toutes ces expériences qui vont être décrites, il est toujours supposé que l'intensité des sources lumineuses utilisées est très faible, de telle sorte que l'aspect quantique du rayonnement peut toujours être mis en évidence. Notamment les détecteurs ou récepteurs de lumière sont des photo-multiplicateurs qui peuvent détecter et compter les photons.

Soit donc une onde électro-magnétique incidente de caractéristiques bien déterminées, et donc constituée de photons identiques. Là où par exemple la physique classique affirme que cette onde se partage en une onde réfléchie et une onde transmise ou réfractée, la physique quantique considère que chacun des photons incidents identiques a une probabilité $\mathcal{P}_r$ d'être réfléchi et une probabilité $\mathcal{P}_t$ d'être transmis :

$$\mathcal{P}_r+ \mathcal{P}_t ~=~ 1$$

de telle sorte que les puissances réfléchies $P_r$ ou transmises $P_t$ sont dans les mêmes rapports que les nombres $N$ de photons correspondants et dans les mêmes rapports que les probabilités associées :

$$\frac{\mathrm{Puissance~r\acute{e}fl\acute{e}chie}}{\mathrm{Puiss... ...~=~ \frac{P_r}{P_t} ~=~ \frac{N_r}{N_t} ~=~ \frac{\mathcal{P}_r}{\mathcal{P}_t}$$

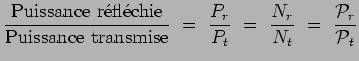Chacune de ces probabilités $\mathcal{P}$ caractérise la probabilité d'un événement ou d'un processus conformément au postulat III de la mécanique quantique. Une telle probabilité est égale au carré du module d'un nombre complexe $Z$ qui mesure l'amplitude de probabilité correspondante. Ce nombre complexe peut lui-même être représenté par un vecteur $\vec{z}$ dans le plan complexe, de telle sorte que :

$$\mathcal{P} ~=~ \begin{array}{\vert c\vert}Z\\ \end{array}^{\,2} ~=~ \begin{array}{\vert c\vert}\vec{z}\\ \end{array}^{\,2}$$

Grâce à cette représentation, les règles d'addition et de multiplication des amplitudes de probabilité pourront être représentées par des constructions vectorielles dans le plan complexe.