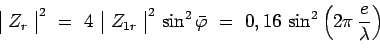


suivant: 3) Sur un miroir
monter: Réflexion et transmission de
précédent: 1) Sur une interface
Table des matières
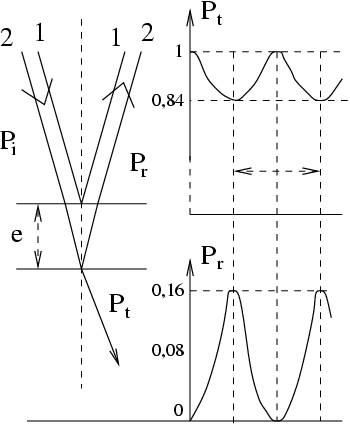
Ces résultats indiquent que les probabilités associées aux voies 1 et 2 ne s'ajoutent pas mais suggèrent
l'interprétation quantique, selon laquelle ce sont les amplitudes de probabilité qui s'ajoutent, et par exemple :
Il devient alors nécessaire de faire appel à un modèle
théorique pour exprimer mathémati-quement l'amplitude 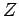 correspondant à chacune des voies que peut emprunter le
processus dont on observe en fait seulement l'état initial
(émission d'un photon par la source
correspondant à chacune des voies que peut emprunter le
processus dont on observe en fait seulement l'état initial
(émission d'un photon par la source 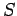 ) et l'état final
(détection à l'aide de deux photo-multiplicateurs des photons
réfléchis ou transmis).
Ici, et dans la suite, le déroulement des processus
considérés est aussi un déroulement temporel. Toutefois,
nous verrons plus tardII28 pourquoi ce
rôle du temps peut être simplement pris en compte, en
admettant que l'amplitude associée à une durée
) et l'état final
(détection à l'aide de deux photo-multiplicateurs des photons
réfléchis ou transmis).
Ici, et dans la suite, le déroulement des processus
considérés est aussi un déroulement temporel. Toutefois,
nous verrons plus tardII28 pourquoi ce
rôle du temps peut être simplement pris en compte, en
admettant que l'amplitude associée à une durée 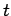 et à un
chemin de longueur
et à un
chemin de longueur 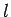 est de la forme :
est de la forme :
le module 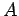 , fonction décroissante de
, fonction décroissante de 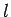 , étant presque constant et
, étant presque constant et 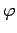 étant proportionnel
à la durée
étant proportionnel
à la durée 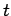 du trajet ou au nombre
du trajet ou au nombre 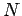 de longueurs d'onde
de longueurs d'onde 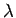 que contient sa longueur
que contient sa longueur 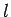 :
:
De plus, il sera expliqué dans la suite, pourquoi l'amplitude 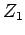 associée à la réflexion sur la première
interface doit être multipliée par
associée à la réflexion sur la première
interface doit être multipliée par 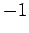 .
.
|
Ce modèle extrêmement rudimentaire fournit immédiatement
une méthode de construction vectorielle de l'amplitude 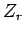 :
:
avec :
|
|
et rend compte immédiatement du caractère
oscillatoire de la probabilité :
représenté sur les courbes précédentes. Si la
lumière incidente est blanche et si l'épaisseur de la lame
n'est pas constante, on remarque que la couleur principalement
réfléchie dépend de cette épaisseur, ce qui donne
naissance aux phénomènes d'irisation (anneaux de
Newton).



suivant: 3) Sur un miroir
monter: Réflexion et transmission de
précédent: 1) Sur une interface
Table des matières
Arnaud Balandras
2005-04-02
![]() correspondant à chacune des voies que peut emprunter le
processus dont on observe en fait seulement l'état initial
(émission d'un photon par la source
correspondant à chacune des voies que peut emprunter le
processus dont on observe en fait seulement l'état initial
(émission d'un photon par la source ![]() ) et l'état final
(détection à l'aide de deux photo-multiplicateurs des photons
réfléchis ou transmis).
Ici, et dans la suite, le déroulement des processus
considérés est aussi un déroulement temporel. Toutefois,
nous verrons plus tardII28 pourquoi ce
rôle du temps peut être simplement pris en compte, en
admettant que l'amplitude associée à une durée
) et l'état final
(détection à l'aide de deux photo-multiplicateurs des photons
réfléchis ou transmis).
Ici, et dans la suite, le déroulement des processus
considérés est aussi un déroulement temporel. Toutefois,
nous verrons plus tardII28 pourquoi ce
rôle du temps peut être simplement pris en compte, en
admettant que l'amplitude associée à une durée ![]() et à un
chemin de longueur
et à un
chemin de longueur ![]() est de la forme :
est de la forme :
![]() , fonction décroissante de
, fonction décroissante de ![]() , étant presque constant et
, étant presque constant et ![]() étant proportionnel
à la durée
étant proportionnel
à la durée ![]() du trajet ou au nombre
du trajet ou au nombre ![]() de longueurs d'onde
de longueurs d'onde ![]() que contient sa longueur
que contient sa longueur ![]() :
:
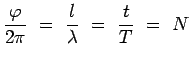
![]() associée à la réflexion sur la première
interface doit être multipliée par
associée à la réflexion sur la première
interface doit être multipliée par ![]() .
.