A tout crochet de Poisson classique ![]() Dirac fait correspondre un crochet de Poisson quantique
noté
Dirac fait correspondre un crochet de Poisson quantique
noté ![]() :
:
et il est postulé que ces crochets de Poisson quantiques satisfont les mêmes
relations que leurs homologues classiques, à condition de toujours respecter
l'ordre des facteurs dans un produit. C'est ce qui a été fait
précédemment, de telle sorte que ces relations sont également satisfaites
par les crochets quantiques. Dès lors,
![]() désignant quatre
observables quelconques, il en résulte :
désignant quatre
observables quelconques, il en résulte :
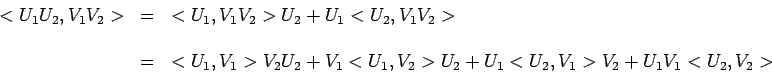 |
mais encore également :
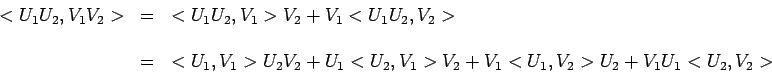 |
En exprimant l'identité des deux expressions ainsi obtenues, on écrit :
et puisque ![]() et
et ![]() sont indépendants de
sont indépendants de ![]() et
et ![]() :
:
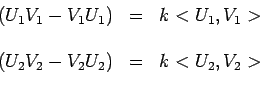 |
Puisque ![]() ne doit dépendre ni de
ne doit dépendre ni de ![]() et
et ![]() , ni de
, ni de ![]() et
et ![]() , et
doit commuter avec
, et
doit commuter avec ![]() quels que soient
quels que soient ![]() et
et ![]() ,
, ![]() est une
constante et très généralement on peut écrire,
est une
constante et très généralement on peut écrire, ![]() et
et ![]() désignant
deux observables quelconques :
désignant
deux observables quelconques :