Application

Soit une particule de coordonnées $q_i=(x,y,z)$ et d'impulsions $p_i=(p_x,p_y,p_z)$ . On remarque :

$$\left(q_i,q_j\right)=0~~~~~~~\left(q_i,p_j\right)=\delta_{ij}~~~~~~~ \left(p_i,p_j\right)=0$$

Il en résulte que les observables images satisfont les relations suivantes qui se révèleront fondamentales :

$$\left[X,P_x\right]=\left[Y,P_y\right]=\left[Z,P_z\right]=i\hbar$$

tous les autres commutateurs étant nuls.

Etant donné, comme il a déjà été dit, que toute variable dynamique classique d'un système, fonction des variables fondamentales $q_i$ et $p_j$ , est exprimable en série de puissance de ces $q_i$ et $p_j$ , le commutateur de deux observables, images de deux grandeurs classiques, peut toujours être calculé à partir des commutateurs de base entre les observables images de ces $q_i$ et $p_j$ . Considérons, par exemple, les composantes du moment cinétique d'une particule :

$$\begin{array}{ccccccc} \ell_x & = & y\,p_z-z\,p_y & ~~~\Longr... ...ow~~~ & L_z & = & X\,P_y-Y\,P_x \\ & & & & & & \\ \end{array}$$

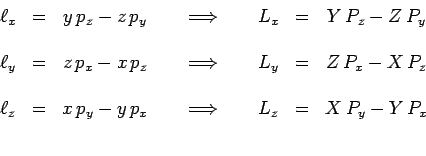d'où il résulte par exemple :

$$\left[L_x,L_y\right] = \left[Y\,P_z-Z\,P_y,Z\,P_x-X\,P_z\right]$$

en ne gardant que les commutateurs non nuls :

$$\left[L_x,L_y\right] = Y\left[P_z,Z\right]P_x+X\left[Z,P_z\right]P_y = i\hbar\,\left(X\,P_y-Y\,P_x\right)$$

d'où :

$$\left[L_x,L_y\right] = i\hbar\,L_z$$

Question 3-2 : Calculez les commutateurs $\left[L_x,Y\right]$ et $\left[L_x,P_y\right]$ .

Question 3-3 : Considérez un rotateur plan (par exemple une molécule diatomique $H^2$ autour de son centre de masse). Ecrire sa fonction de Lagrange, et le moment conjugué $p_\theta$ de la variable angulaire $\theta$ . Calculez le commutateur $\left[\theta,p_\theta\right]$ .