Signification physique

L'inégalité de Heisenberg révèle qu'en général la mesure sur un état physique $\Psi$ quelconque de deux observables $A$ et $B$ quelconques, qui ne commutent pas, ne peut donner deux valeurs toutes deux bien définies. C'est-à-dire que dans cet état $\Psi$ on ne peut trouver en même temps :

$$\hat{A}=a~~~~~~\mathrm{et}~~~~~~\hat{B}=b$$

Cette affirmation ne signiife pas qu'il serait seulement impossible de mesurer en même temps^III5 $A$ et $B$ , en raison éventuellement de perturbations dues aux mesures.

L'inégalité de Heisenberg :

$$\Delta A.\Delta B\geq\frac{\hbar}{2}\,\alpha~~~~~~~\alpha\,\in\,\mathbf{R}$$

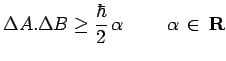signifie qu'il n'existe pas de vecteur ket du type $\mid a,b>$ qui serait en même temps vecteur propre de $A$ et de $B$ :

$$A\,\mid a,b>=a\,\mid a,b>~~~~~\mathrm{et}~~~~~B\,\mid a,b>=b\,\mid a,b>$$

et puisque ce vecteur ket n'existe pas, il n'existe pas non plus, en vertu du postulat I, d'état physique correspondant.

Question 3-6 : Montrez qu'en particulier, un vecteur propre du type $\mid \omega>=\mid x,p_x>$ commun aux observables $X$ et $P_x$ ne peut exister. A cet effet :

$\imath-$ Calculez $\left(X\,P_x-P_x\,X\right)\,\mid \omega>$ et $i\hbar\,\mid \omega>$ . Comparez.

$\imath\imath-$ Calculez $\Delta X$ et $\Delta P_x$ .

Une inégalité de Heisenberg du type :

$$\Delta X.\Delta P_x\geq\frac{\hbar}{2}$$

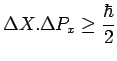signifie en particulier que la dispersion $\Delta X$ sur les valeurs de $X$ est d'autant plus grande que celle $\Delta P_x$ sur les valeurs de $P_x$ est plus faible, et inversement, et qu'il n'existe aucun état possible $\Psi$ de la particule, tel que le produit de ces deux dispersions soit inférieur à $\frac{\hbar}{2}$ . En particulier :

Avec $\mid \Psi>$ =	$\mid x,y,z>$	$\mid p_x,p_y,p_z>$
$\Delta X$	0	$+\infty$
$\Delta Y$	0	$+\infty$
$\Delta Z$	0	$+\infty$
$\Delta P_x$	$+\infty$	0
$\Delta P_y$	$+\infty$	0
$\Delta P_z$	$+\infty$	0