Transformations infinitésimales

Toute transformation $\mathcal{T}$ voisine de l'identité s'appelle une transformation infinitésimale et, dans le cas où elle ne dépend que d'un seul paramètre réel, peut s'écrire :

$$\mathcal{T}(\varepsilon)=\mathbf{1}+\varepsilon.\tau$$

$\mathbf{1}$ désignant l'opérateur unité, et $\tau$ un opérateur appelé le générateur infinitésimal des transformations $\mathcal{T}$ . On notera :

$$\mathrm{Puisque}~~~~~~\mathcal{T}^{-1}=\mathcal{T}^\dagger~~~~~~~~~~~~~ \mathbf{1}-\varepsilon.\tau=\mathbf{1}+\varepsilon.\tau^\dagger$$

$$\mathrm{donc}~~~~~~\tau^\dagger=-\tau$$

et $\tau$ est antihermitique.

On aurait pu également écrire :

$$\mathcal{T}(\varepsilon)=\mathbf{1}+i\,\varepsilon.\tau^\prime$$

Puisque $\mathcal{T}^{-1}=\mathcal{T}^\dagger$ alors :

$$\mathbf{1}-i\,\varepsilon.\tau^\prime= \mathbf{1}-i\,\varepsilon.\tau^{\prime\dagger}$$

donc $\tau^\prime=\tau^{\prime\dagger}$ et $\tau^\prime$ est hermitique.

L'intérêt des transformations infinitésimales est qu'elles peuvent engendrer les transformations finies. En effet, si $a$ désinge une valeur finie du paramètre et si on peut écrire :

$$\mathcal{T}(a)=\left[\mathcal{T}\left(\frac{a}{n}\right)\right]^n$$

autrement dit, si le paramètre est additif, on peut alors écrire :

$$\mathcal{T}(a)=\lim_{n\to\infty}\,\left(\mathbf{1}+\frac{a}{n}\,\tau\right)^n= e^{a\,\tau}=e^{ia\,\tau^\prime}$$

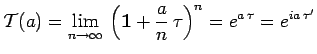de la forme :

$\mathcal{U}=e^{i\,h}$

On notera la relation entre un opérateur hermitique $h$ et un opérateur unitaire $\mathcal{U}$ :

$$h^\dagger=h~~~~~~~~~~~~\mathcal{U}^\dagger=\mathcal{U}^{-1}$$

Question 3-10 : Considérez la transformation de Lorentz :

   

$$\left\lbrace \begin{array}{l} x^\prime = \gamma\,(x-v\,t) \\ ... ... t^\prime = \gamma\,(t-\frac{v}{c^2}\,x) \\ \end{array}\right.$$

$~~~\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$

   Ecrire l'opérateur $T(v)$ correspondant sous la forme matricielle. Le paramètre $v$ est-il additif ? Savez-vous le remplacer par un autre paramètre additif ?