Générateurs des translations

Ainsi, dans l'ensemble des observables considérées initialement, toute observable $\Omega$ autre que $X$ est invariante dans les translations $T_x$ de direction $O\vec{x}$ et donc commute avec le générateur $d_x$ :

$$\left\lbrace \begin{array}{lcrcl} \Omega_d=\Omega & ~~~~\long... ...grightarrow~~~~ & [d_x,X] &=&-\mathbf{1} \\ \end{array}\right.$$

Or, nous connaissons une observable jouissant des mêmes propriétés de commutation, c'est l'observable $P_x$ .

Question 3-11 : En utilisant la méthode de Dirac, motrez que $P_x$ commute avec toutes les observables $\Omega$ autres que $X$ ou fonctions de $X$ de telle sorte que :

$$[X,P_x]=i\,\hbar~~~~~~~~~~~~[\Omega,P_x]=0$$

Il en résulte que l'opérateur hermitique :

$$P_x-i\,\hbar\,d_x~~~~~~~~~~~~~~~~~~~~~~~~(d_x^\dagger=-d_x)$$

commute avec toutes les observables du système. On démontre qu'un tel opérateur ne peut être qu'un nombre pur (et donc réel puisque hermitique) :

$$P_x-i\,\hbar\,d_x=r$$

et en ramplçant $d_x$ (défini à un nombre additif imaginaire pur près) par :

$$\left\lbrace \begin{array}{lcl} d_x & ~~~~\longrightarrow~~~~... ...bar\,(d_x-\frac{i}{\hbar}\,r) = r - r = 0\\ \end{array}\right.$$

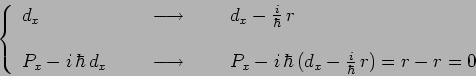On obtient ainsi l'expression du générateur infinitésimal $d_x$ en fonction de la composante $x$ de l'impulsion totale $P_x$ du système considéré :

$d_x=-\frac{i}{\hbar}\,P_x$

De l'expression de l'opérateur de translation infinitésimale :

$$\mathcal{D}_x(\delta x)=\mathbf{1}-\frac{i}{\hbar}\,\delta x.P_x$$

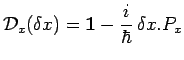on déduit celle de l'opérateur de translation induite pour une translation finie :

$$\mathcal{D}_x(a)=\lim_{n\to\infty}\,\left[\mathcal{D}_x(\frac{a}{... ... \lim_{n\to\infty}\,\left(\mathbf{1}-\frac{i}{\hbar}\,\frac{a}{n}\,P_x\right)^n$$

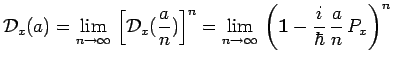et tenu compte de la relation mathématique :

$$\lim_{n\to\infty}\,\left(1+\frac{x}{n}\right)^n=e^x$$

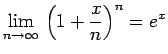qui peut être ici généralisée pour des opérateurs, on obtient :

$\mathcal{D}_x(a)=e^{-\frac{i}{\hbar}\,a\,P_x}$

Question 3-12 : Démontrez que dans une translation d'axe $O\vec{x}$ et de longueur $a$ :

$$X~~~~~~\longrightarrow~~~~~~X^\prime=\mathcal{D}_x(a)\,X\,\mathcal{D}^{-1}_x(a)= X-a$$

Considérons le produit de trois translations effectuées successivement dans l'espace physique, et de longueurs $a_z$ selon $O\vec{z}$ , $a_y$ selon $O\vec{y}$ et $a_x$ selon $O\vec{x}$ . L'opérateur de translation induite s'écrira alors :

$$\mathcal{D}_x(a_x)\,\mathcal{D}_y(a_y)\,\mathcal{D}_z(a_z)= e^{-\... ...ar}\,a_x\,P_x}\,e^{-\frac{i}{\hbar}\,a_y\,P_y}\, e^{-\frac{i}{\hbar}\,a_z\,P_z}$$

Question 3-13 : Démontrez que si et seulement si $[A,B]=0$ :

$$e^A\,.\,e^B=e^{A+B}$$

Tenu compte du résultat précédent et sachant que les composantes de l'impulsion totale commutent, on en déduit avec :

$$\vec{a}=a_x\,\vec{x}+a_y\,\vec{y}+a_z\,\vec{z}=\lambda\,\vec{u}$$

$$\mathcal{D}_x(a_x)\,\mathcal{D}_y(a_y)\,\mathcal{D}_z(a_z)=\mathcal{D}(\vec{a})$$

avec :

$$\mathcal{D}(\vec{a})=e^{-\frac{i}{\hbar}\,\vec{a}.\vec{P}}= e^{-\frac{i}{\hbar}\,\lambda\,P_u}$$

On se rappellera que cette dernière expression est celle d'une translation induite active, c'est-à-dire imposée à un système.

Problème : Transformations de Galilée, cf. Compléments.

Ainsi, connaitre un seul opérateur $P_x$ : la composante $x$ de l'impulsion totale du système, suffit pour connaitre tous les opérateurs $\mathcal{D}_x$ de translation dans la direction $O\vec{x}$ . $P_x$ est bien le générateur de toutes les translations induites. Il en est évidemment de même des translations dans les directions $O\vec{y}$ et $O\vec{z}$ .