Rotations dans l'espace physique

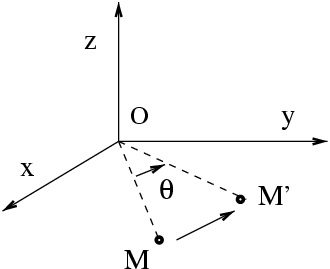
Dans une rotation active autour de l'axe $O\vec{z}$ et d'un angle $\theta$ : $$\begin{array}{lcl} x^\prime+i\,y^\prime & = & e^{i\,\theta}\,... ...heta+y\,\cos\theta \\ & & \\ z^\prime & = & z \\ \end{array}$$

et pour une rotation infinitésimale $\theta=\delta\theta_z\ll 1$ :

$$M^\prime=(1-i\,\delta\theta_z\,\ell_z)\,M$$

avec :

$$M^\prime=\left(\begin{array}{c} x^\prime \\ y^\prime \\ z^\prime ... ...ght)~~~~~~~~~~~~~~~~M=\left(\begin{array}{c} x \\ y \\ z \\ \end{array}\right)$$

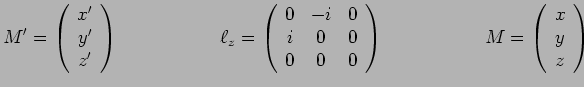On obtient des expressions semblables pour des rotations autour des axes $Ox$ et $Oy$ :

$$\ell_x=\left(\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & -i \\ 0 & ... ...begin{array}{ccc} 0 & 0 & i \\ 0 & 0 & 0 \\ -i & 0 & 0 \\ \end{array}\right)$$

et on remarque :

$$\ell_x\,.\,\ell_y-\ell_y\,.\,\ell_x=[\ell_x,\ell_y]=i\,\ell_z$$

On notera que cette relation n'a aucun caractère quantique. C'est une relation classique concernant les rotations dans l'espace physique à 3 dimensions.

Des rotations infinitésimales, on passe aux rotations finies par itération. La matrice correspondant à une rotation d'un angle fini $\theta$ , autour de l'axe $Oz$ s'écrit en effet :

$$R_z(\theta)=\lim_{n\to\infty}\,\left[R_z(\frac{\theta)}{n})\right]^n= \lim_{n\to\infty}\,\left(\mathbf{1}-i\,\frac{\theta)}{n}\,\ell_z\right)^n$$

d'où :

$R_z(\theta)=e^{-i\,\theta\,\ell_z}$

On notera encore ici que cette expression est parfaitement classique (d'ailleurs la constante $\hbar$ n'est évidemment pas figurée !).

Considérons en particulier la suite des quatre rotations suivantes :

$$R=R_x(\delta)\,R_y(\varepsilon)\,R_x(-\delta)\,R_y(-\varepsilon)=... ...,\varepsilon\,\ell_y}\,.\, e^{i\,\delta\,\ell_x}\,.\,e^{i\,\varepsilon\,\ell_y}$$

qui ne produirait aucune rotation résultante si ces rotations commutaient entre elles. En considérant les angles $\varepsilon$ et $\delta$ très petits ( $\varepsilon\ll 1$ et $\delta\ll 1$ ) il va être utile pour la suite de faire un développement de $R$ jusqu'au second ordre, en développant chaque exponentielle elle-même jusqu'au second ordre, soit par exemple :

$$e^{-i\,\delta\,\ell_x}=\mathbf{1}-i\,\delta\,\ell_x+ \frac{(-i\,\delta)^2}{2!}\,\ell_x^2$$

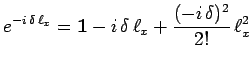On obtient, alors, tout clacul fait, et en se limitant toujours au second ordre :

$$R=\mathbf{1}-\delta\,\varepsilon\,(\ell_x\,\ell_y-\ell_y\,\ell_x)= \mathbf{1}-i\,.\,\delta\,\varepsilon\,.\,\ell_z$$

Ainsi au second ordre près, la rotation $R$ considérée est équivalente à une rotation d'axe $Oz$ et d'angle $\delta\,\varepsilon$ . Ce résultat va nous servir ci-après.