Supposons maintenant que la rotation précédente
![]() soit
appliquée au système physique étudié
soit
appliquée au système physique étudié
![]() , c'est-à-dire , comme cela a déjà
été précisé, soit appliquée à ses états. Dans cet espace des
états
, c'est-à-dire , comme cela a déjà
été précisé, soit appliquée à ses états. Dans cet espace des
états
![]() , la rotation physique
, la rotation physique
![]() est représentée
mathématiquement par un opérateur de rotation induite
est représentée
mathématiquement par un opérateur de rotation induite
![]() dont nous avons déjà vu qu'il était unitaire :
dont nous avons déjà vu qu'il était unitaire :
et à l'instar de ce qui a déjà été fait pour les
translations, une rotation d'un angle infinitésimal
![]() , c'est-à-dire
voisine de l'identité, pourra s'écrire :
, c'est-à-dire
voisine de l'identité, pourra s'écrire :
![]() désignant l'opérateur générateur infinitésimal des
rotations autour de l'axe
désignant l'opérateur générateur infinitésimal des
rotations autour de l'axe ![]() .
.
Il s'agit de déterminer cet opérteur ![]() . A cet effet on pourrait suivre
la même demarche que celle déjà suivie pour déterminer
. A cet effet on pourrait suivre
la même demarche que celle déjà suivie pour déterminer ![]() . Il
faudrait pour cela examiner comment chacune des observables est transformée
sous l'effet de cette roattion induite. Nous nous bornerons à procéder par
analogie.
. Il
faudrait pour cela examiner comment chacune des observables est transformée
sous l'effet de cette roattion induite. Nous nous bornerons à procéder par
analogie.
Dans le cas d'une translation induite :
le générateur ![]() s'obtient en calculant le moment conjugué de
la variable
s'obtient en calculant le moment conjugué de
la variable ![]() concernée par la translation :
concernée par la translation :
 |
et le générateur ![]() s'en déduit :
s'en déduit :
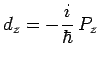 |
Nous admettrons que ce procédé peut être généralisé de telle sorte
que le générateur ![]() de la rotation induite :
de la rotation induite :
peut s'obtenir en calculant le moment conjugué de la variable
![]() : la seule concernée par la rotation autour de
: la seule concernée par la rotation autour de ![]() . Or, nous savons
déjàIII13 qu'en exprimant l'énergie
cinétique en fonction notamment de la variable
. Or, nous savons
déjàIII13 qu'en exprimant l'énergie
cinétique en fonction notamment de la variable ![]() :
:
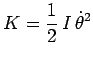 |
que le moment conjugué de cette variable ![]() :
:
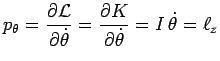 |
n'est autre que la composante ![]() du moment cinétique total du système
, puisque
du moment cinétique total du système
, puisque ![]() repérait lui-même l'orientation du système dans son ensemble,
c'est-à-dire celle de son centre de masse. Conformément au procédé utilisé, le
générateur
repérait lui-même l'orientation du système dans son ensemble,
c'est-à-dire celle de son centre de masse. Conformément au procédé utilisé, le
générateur ![]() s'en déduit immédiatement :
s'en déduit immédiatement :
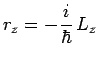 |
Comme précédemment pour les translations, les expressions des opérateurs
des rotations induites infinitésimales et finies s'en déduisent aussitôt :
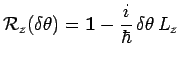 |
![$\displaystyle \mathcal{R}_z(\theta)=\lim_{n\to\infty}\,
\left[\mathcal{R}_z(\frac{\theta}{n})\right]^n=e^{-\frac{i}{\hbar}\,\theta\,L_z}$](img1937.png) |
On remarquera l'analogie de structure entre l'opérateur de rotation
![]() dans l'espace physique
dans l'espace physique
![]() à trois dimensions, et son
image : l'opérateur de rotation induite
à trois dimensions, et son
image : l'opérateur de rotation induite
![]() dans l'espace
des états
dans l'espace
des états
![]() :
:
Toutefois, il y a lieu de remarquer que
![]() (matrice
(matrice ![]() ) agit
dans un espace à trois dimensions, tandis que
) agit
dans un espace à trois dimensions, tandis que
![]() agit
dans un espace de Hilbert
agit
dans un espace de Hilbert
![]() à une infinité de dimensions.
à une infinité de dimensions.