Tout état ![]() de la particule sera repéré sur cette base :
de la particule sera repéré sur cette base :
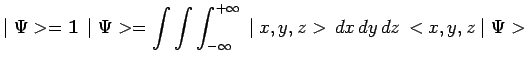 |
par ses composantes
![]() , qui constituent la fonction d'onde
représentative, dont le carré du module, comme nous l'avons déjà
remarqué, est égal à la densité de probabilité de localisation de la
particule :
, qui constituent la fonction d'onde
représentative, dont le carré du module, comme nous l'avons déjà
remarqué, est égal à la densité de probabilité de localisation de la
particule :
Question 3-19 : Soit, dans un espace à une dimension, une particule dont
l'état ![]() est représenté par la fonction d'onde :
est représenté par la fonction d'onde :
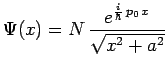 |
![]() ,
, ![]() et
et ![]() désignant trois constantes réelles.
désignant trois constantes réelles.
![]() Déterminez
Déterminez ![]() pour que
pour que ![]() soit normé.
soit normé.
![]() On mesure la position de la particule. Quelle est la
probabilité pour que le résultat soit compris entre
On mesure la position de la particule. Quelle est la
probabilité pour que le résultat soit compris entre
![]() et
et
![]() ?
?
![]() Quelle est la valeur moyenne de l'impulsion de la
particule dans l'état
Quelle est la valeur moyenne de l'impulsion de la
particule dans l'état ![]() ?
?
Le vecteur bra ![]() est représenté par la fonction
d'onde complexe conjuguée :
est représenté par la fonction
d'onde complexe conjuguée :
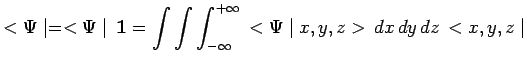 |
avec :
tandis qu'un produit scalaire est repésenté par une intégrale de
recouvrement :
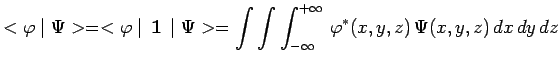 |
Puisque tout ket ![]() est parfaitement défini par sa fonction d'onde
représentative, nous pourrons dans la suite abandonner les notations de Dirac
et remplacer la notion vecteur ket
est parfaitement défini par sa fonction d'onde
représentative, nous pourrons dans la suite abandonner les notations de Dirac
et remplacer la notion vecteur ket ![]() par la notion fonction
d'onde
par la notion fonction
d'onde
![]() :
:
Il faut alors préciser la nouvelle notation concernant les observables.