Considérons d'abord l'une, par exemple ![]() , des observables de
base. L'opérateur
, des observables de
base. L'opérateur ![]() agissant sur un vecteur ket
agissant sur un vecteur ket ![]() le
transforme en un autre vecteur
le
transforme en un autre vecteur
![]() , dont il s'agit de
déterminer la fonction d'onde. à savoir :
, dont il s'agit de
déterminer la fonction d'onde. à savoir :
de telle sorte que, dans les cas simples, les règles de
transcription des notations de Dirac dans la représentation de Schrödinger,
s'écrivent par exemple :
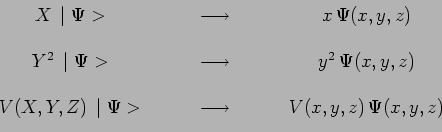 |
Considérons maintenant les observables
![]() composantes de
l'impulsion de la particule. Il s'agit de déterminer la transcription :
composantes de
l'impulsion de la particule. Il s'agit de déterminer la transcription :
![]() désignant un opérateur fonctionnel,
agissant sur la fonction
désignant un opérateur fonctionnel,
agissant sur la fonction
![]() . A cet effet, il y a lieu
de se souvenir que l'opérateur
. A cet effet, il y a lieu
de se souvenir que l'opérateur ![]() est le générateur des
translations le long de l'axe
est le générateur des
translations le long de l'axe ![]() et transforme un état
et transforme un état
![]() représenté par le ket
représenté par le ket ![]() ``chez Dirac'', ou la
fronction d'onde
``chez Dirac'', ou la
fronction d'onde
![]() ``chez Schrödinger '' en un ket
``chez Schrödinger '' en un ket
![]() ou une fonction d'onde
ou une fonction d'onde
![]() de telle
sorte que l'opérateur de déplacement peut sécrire des deux
manières suivantes, et ceci pour une translation
infinitésimale :
de telle
sorte que l'opérateur de déplacement peut sécrire des deux
manières suivantes, et ceci pour une translation
infinitésimale :
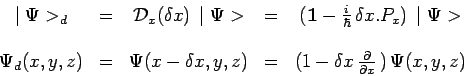 |
En comparant les deux seconds membres on en déduit immédiatement la règle
de transcription cherchée :
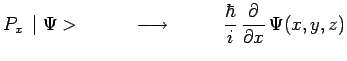 |
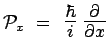
|
et plus généralement, en notation vectorielle symbolique :
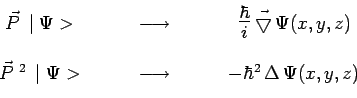 |
Question 3-20 : En utilisant la représentation de Schrödinger des
opérateurs, démontrez :
![$\displaystyle [X,P_x]=i\,\hbar~~~~~~~~~~~~~~~~~~~~~~~~[P_x,V(X,Y,Z)]~~~\longrightarrow~~~
\frac{\hbar}{i}\,\frac{\partial}{\partial x}\,V(x,y,z)$](img1976.png) |
L'expression de toutes les autres observables, fonctions des variables de
position et d'impulsion, en résulte immédiatement, et par exemple pour
l'énergie totale de la particule, plongée dans un champ de potentiel, tel que son
énergie potentielle s'écrit :
| Energie | Classique | Dirac | Schrödinger |
| Cinétique |
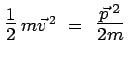
|
|
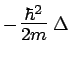
|
| Potentielle |
d'où résulte pour l'énergie totale :
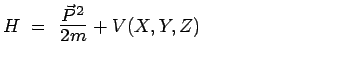
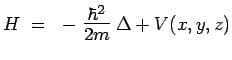
|
L'observable énergie ![]() , écrite à la manière de Hamilton s'appelle le
hamiltonien.
, écrite à la manière de Hamilton s'appelle le
hamiltonien.