La représentation de Schrödinger

Choisir une représentation, c'est donner une représentation numérique des êtres mathéma-tiques : kets, bras, opérateurs,... etc utilisés dans le formalisme. C'est représenter chacun de ces êtres par un ensemble de nombres et pour le faire, comme nous l'avons déjà vu, il faut choisir un E.C.O.C. dont les vecteurs propres communs constituent une base bien définie dans l'espace des états. Tous ces E.C.O.C. sont mathématiquement équivalents, et de ce point de vue les observables de position $X,~Y,~Z$ ou d'impulsion $P_x,~P_y,~P_z$ ne jouissent plus du privilège dont ils bénéficiaient dans la physique classique, du fait que l'espace de référence était alors l'espace physique à trois dimensions. Au contraire, en mécanique quantique, l'espace support de toute représentation est un espace abstrait mathématique purement opérationnel, puisqu'il change avec le système physique étudié.

Toutefois, puisque tout état est repéré par rapport aux états de base, il est préférable que ces derniers jouissent de propriétés physiques bien définies, de manière à constituer une bonne interface entre la théorie et la pratique expérimentale. A cet effet il y a intérêt à choisir pour états de base les états propres d'un E.C.O.C. constitué avec des observables choisies parmi les observables de position et d'impulsion. C'est ce qui va être fait ci-après.

Considérons le système simple constitué d'une particule de spin nul (ou sans spin). Pour un tel système, les observables de position $X,~Y,~Z$ suffisent pour constituer un E.C.O.C. et leurs vecteurs propres communs :

$$\mid x,y,z>~~~~~~~~~~~~~~~~~~~~~~~~-\infty\leq x,y,z \leq +\infty$$

contituent la base de représentation de Schrödinger. Ces vecteurs de base seront supposés normalisés à la manière de Dirac :

$$<x^\prime,y^\prime,z^\prime\mid x,y,z>= \delta(x^\prime-x).\delta(y^\prime-y).\delta(z^\prime-z)$$

de telle sorte que la relation de fermeture s'écrit :

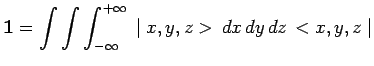$$\mathbf{1}=\int\int\int_{-\infty}^{+\infty}\,\mid x,y,z>\, dx\,dy\,dz\,<x,y,z\mid$$