|
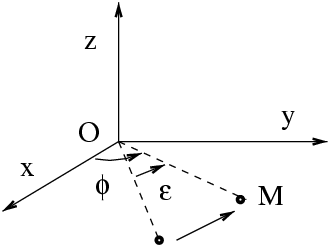
Dans la rotation infinitésimale
|
Supposons que chaque état de cette particule puisse être caractérisé par une seule fonction d'onde :
|
|
et en développant le second membre :
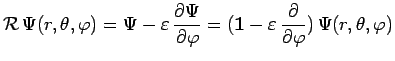 |
En comparant avec l'expression de
![]() , qui définit le moment
angulaire total de ce système, on en déduit :
, qui définit le moment
angulaire total de ce système, on en déduit :
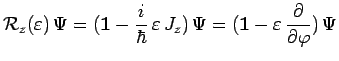 |
d'où :
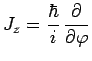 |
Cette expression est celle de ![]() , dans la représentation de Schrödinger, que
nous avons choisie ici, en représentant l'état de la particule par sa
fonction d'onde.
, dans la représentation de Schrödinger, que
nous avons choisie ici, en représentant l'état de la particule par sa
fonction d'onde.
Toutefois, il y a lieu de remarquer que, conformément aux règles de
changement de variables :
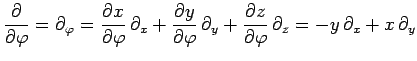 |
d'où :
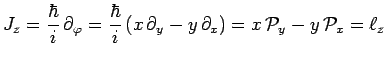 |
et plus généralement dans toute représentation :
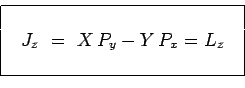 |
Dans ce cas particulièrement simple, le moment angulaire total ![]() du
système se réduit au simple moment orbital
du
système se réduit au simple moment orbital ![]() . On dit que le système a un
spin nul ou n'a pas de spin.
. On dit que le système a un
spin nul ou n'a pas de spin.