Considérons maintenant un système dont chaque état ne peut pas
être caractérisé par une seule fonction d'onde, mais par
trois fonctions d'onde du type de la précédente et dont
chacune est associée à une des trois directions ![]() d'un
trièdre de référence :
d'un
trièdre de référence :
Supposons de plus, que ces trois composantes de l'état physique considéré, se transforment dans les rotations comme les trois composantes d'un vecteur.
Le système précédent pourrait être par exemple le champ magnétique ou le champ électrique. Il peut également comme nous allons le voir être une particule, mais cette particule est alors d'une nature plus complexe que celle considérée précédemment, puisque cette particule possède maintenant une sorte d'orientation intrinsèque dans l'espace.
|
|
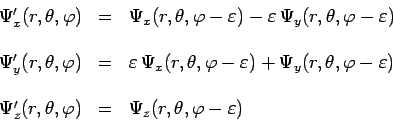 |
En développant au premier ordre en
![]() seulement, et tenu compte des
résultats précédents :
seulement, et tenu compte des
résultats précédents :
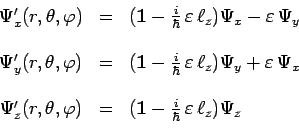 |
que l'on peut encore écrire symboliquement :
![$\displaystyle \vec{\Psi}^\prime=
\left[\mathbf{1}-\frac{i}{\hbar}\,\varepsilon\,(\ell_z+S_z)\right]\,\vec{\Psi}$](img2042.png) |
![]() désignant une matrice telle que :
désignant une matrice telle que :
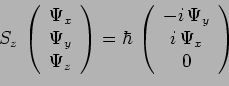 |
Ainsi ![]() transforme chaque composante en un point donné, en
une combinaison linéaire particulière des trois composantes au
même point. Le vecteur
transforme chaque composante en un point donné, en
une combinaison linéaire particulière des trois composantes au
même point. Le vecteur ![]() étant défini par
ses trois composantes cartésiennes
étant défini par
ses trois composantes cartésiennes ![]() avec
avec
![]() l'opérateur
l'opérateur ![]() est représenté par la
matrice :
est représenté par la
matrice :
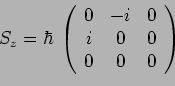 |
On définirait de même les opérateurs ![]() et
et ![]() associés aux
rotations d'axes
associés aux
rotations d'axes ![]() et
et ![]() et on obtiendrait alors :
et on obtiendrait alors :
 |
La comparaison du résultat obtenu avec l'expression générale de
l'opérateur de rotation, qui définit le moment angulaire total du
système :
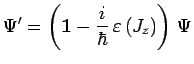 |
indique l'expression de ![]() dans une représentation quelconque :
dans une représentation quelconque :
et du moment angulaire total :
Les composantes
![]() de l'opérateur
de l'opérateur ![]() ayant
été données ci-dessus, il est facile de montrer que
l'opérateur vectoriel
ayant
été données ci-dessus, il est facile de montrer que
l'opérateur vectoriel ![]() est bien un moment
angulaire. En effet on vérifie aisément sur les formes
matricielles :
est bien un moment
angulaire. En effet on vérifie aisément sur les formes
matricielles :
et par ailleurs :
Ainsi, dans le cas particulier du système étudié ici, le moment angulaire
total ![]() est la somme du moment angulaire orbital déjà
défini précédemment
est la somme du moment angulaire orbital déjà
défini précédemment ![]() et d'un autre moment angulaire intrinsèque
et d'un autre moment angulaire intrinsèque
![]() que l'on appelle le spin du système. Le système ici considéré,
et doté de trois composantes, a un spin égal à 1.
que l'on appelle le spin du système. Le système ici considéré,
et doté de trois composantes, a un spin égal à 1.
La fonction d'onde d'une particule de spin 1 est donc de la forme :
![]() désignant alors une fonction d'onde dépendant
non seulement des variables de position, mais d'un indice
désignant alors une fonction d'onde dépendant
non seulement des variables de position, mais d'un indice ![]() à
trois valeurs, qui constitue une sorte de variable interne
qui permet de décrire l'orientation dans l'espace de la
particule.
à
trois valeurs, qui constitue une sorte de variable interne
qui permet de décrire l'orientation dans l'espace de la
particule.
Le produit scalaire de deux fonctions de ce type sera de la forme :
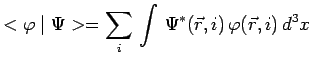 |
Un opérateur tel que ![]() agit sur les variables de position seulement,
tandis que
agit sur les variables de position seulement,
tandis que ![]() agit sur la variable interne
agit sur la variable interne ![]() seulement. Deux tels
opérateurs agissant sur des variables ditinctes commutent toujours.
seulement. Deux tels
opérateurs agissant sur des variables ditinctes commutent toujours.
On remarquera que les vecteurs unitaires
![]() des axes sont des vecteurs propres de
des axes sont des vecteurs propres de
![]() avec la
valeur propre 0
:
avec la
valeur propre 0
:
Sur la base formée de ces vecteurs propres la fonction d'onde se
développe comme suit :
Une base plus traditionnelle consiste à prendre les vecteurs
propres de ![]() associés aux valeurs propres
associés aux valeurs propres ![]() soit
soit
![]() :
:
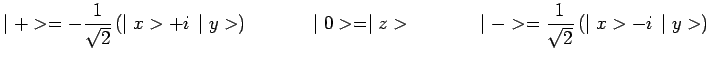 |
et sur cette nouvelle base :
avec :
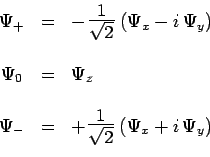 |
On comprend maintenant pourquoi le nombre de composantes est égal à trois
quand le spin est égal à 1. En effet, le nombre de composantes
indépendantes doit être égal au nombre de dimensions de l'espace de spin,
qui est lui-même égal au nombre ![]() de valeurs propres distinctes de
de valeurs propres distinctes de
![]() , dont les vecteurs propres constituent précisément la base.
, dont les vecteurs propres constituent précisément la base.
Question 3-23: Calculez les nouvelles expressions
matricielles prises par les opérateurs ![]()
![]()
![]() sur
la nouvelle base constituée des vecteurs
sur
la nouvelle base constituée des vecteurs
![]() . Vérifiez les relations suivantes :
. Vérifiez les relations suivantes :
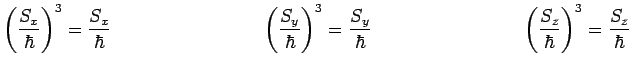 |