|
|
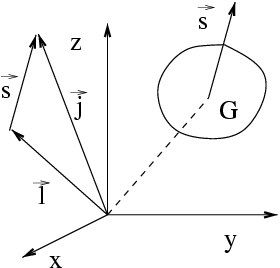
Déjà en mécanique classique, le moment cinétique total, en un point
|
|
|
En mécanique quantique on va retrouver une décomposition mathématique analogue sans que
l'interprétation classique, concrète et imagée, qui vient d'être
rappelée, puisse demeurer valable. En effet, pour tout système physique, y compris
une particule élémentaire on écrira :
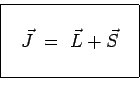 |
![]() désignant le moment cinétique total appelé moment
angulaire total,
désignant le moment cinétique total appelé moment
angulaire total, ![]() désignant le moment orbital et
désignant le moment orbital et ![]() le spin.
Ce spin peut difficilement être considéré comme un moment cinétique
intrinsèque classique lorsque la particule est ponctuelle.
le spin.
Ce spin peut difficilement être considéré comme un moment cinétique
intrinsèque classique lorsque la particule est ponctuelle.
Par ailleurs, tous ces moments angulaires sont quantifiés et leurs composantes sont des opérateurs hermitiques. Ils n'ont qu'un lointain rapport avec les vecteurs classiques correspondants. Leur représentation par des vecteurs est une faute de notation, puisqu'ils ne se comportent pas comme des vecteurs mathématiques. Ce sont des observables vectorielles.
Conformément à ce qui précède, l'expression quantique du
moment angulaire total ![]() d'un système se révèle dans la
manière dont se transforment les vecteurs kets images des
états physiques de ce système, sous l'effet des rotations induites
d'un système se révèle dans la
manière dont se transforment les vecteurs kets images des
états physiques de ce système, sous l'effet des rotations induites
![]() dans cet espace des états, par les
rotations actives
dans cet espace des états, par les
rotations actives
![]() appliquées à ce système dans
l'espace physique :
appliquées à ce système dans
l'espace physique :
Par définition, les composantes
![]() de ce moment angulaire
total sont les générateurs des rotations induites.
de ce moment angulaire
total sont les générateurs des rotations induites.
Pour déterminer le moment angulaire total ![]() d'un système, il suffit
donc d'examiner comment se transforment les états de ce système sous l'effet des
rotations actives.
d'un système, il suffit
donc d'examiner comment se transforment les états de ce système sous l'effet des
rotations actives.
En particulier, pour une rotation infinitésimale autour de l'axe ![]() , on
devra écrire :
, on
devra écrire :
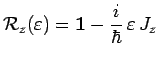 |
et cette expression de
![]() définit
définit ![]() .
.