suivant monter précédent table des matières
suivant: Remarque : monter: Illustrations précédent: Illustrations   Table des matières

Transformations de Galilée (actives)

Soit deux référentiels galiléens $ \Sigma$ et $ \Sigma^\prime$ et soit $ \vec{v}$ la vitesse relative constante de $ \Sigma^\prime$ par rapport à $ \Sigma$ .

\epsffile{/home/arnaud/DossierLambert/DossierLambert/Figures/galilee.eps}    
  Les observables $ X^\prime,~P^\prime_x,\ldots$ etc et $ X,~P_x,\ldots$ etc définies respectivement dans $ \Sigma^\prime$ et $ \Sigma$ sont liées entre elles par les mêmes relations qui relient entre elles les grandeurs classiques correspondantes. Ces relations sont les transformations de Galilée.

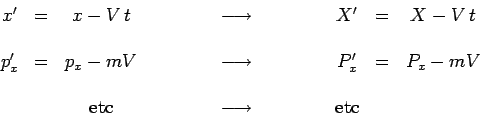\begin{displaymath}\begin{array}{ccccccc} x^\prime &=& x - V\,t & ~~~~~~~~~~\lon... ...athrm{etc} & \longrightarrow & \mathrm{etc} & & \\ \end{array}\end{displaymath}      

Il s'agit de déterminer l'opérateur unitaire $ G$ qui permet de relier les états et les observables $ \mid K>,~A,\ldots$ etc liés à $ \Sigma$ , à ceux $ \mid K^\prime>,~A^\prime,\ldots$ etc liés à $ \Sigma^\prime$ :

$\displaystyle \mid K^\prime>$ $\displaystyle =$ $\displaystyle G\,\mid K>~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~A^\prime\,=\,G\,A\,G^{-1}$  

Considérons à cet effet une transformation infinitésimale de Galilée dans une direction $ x$ donnée :

$\displaystyle G$ $\displaystyle =$ $\displaystyle \mathbf{1} + V\,g$  

$ g$ désignant le générateur infinitésimal de ces transformations. Comme pour les translations et les rotations, ce générateur peut être déterminé à partir de ses relations de commutation avec les observables : $ X~Y~Z~P_x~P_y~P_z~\Omega$ du centre de masse du système physique considéré :

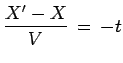$\displaystyle [g,X]$ $\displaystyle =$ $\displaystyle \frac{X^\prime - X}{V} \,=\, -t$  


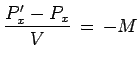$\displaystyle [g,P_x]$ $\displaystyle =$ $\displaystyle \frac{P_x^\prime - P_x}{V} \,=\, -M$  


$\displaystyle [g,\Omega]$ $\displaystyle =$ $\displaystyle 0~~~~~~~~~~~~~~~\mathrm{car}~~~\Omega^\prime\,=\,\Omega$  

On en déduit immédiatement que l'opérateur :

$\displaystyle i\hbar\,g + M\,X -t\,P_x$      

qui commute avec toutes les observables est une constante qui peut être choisie nulle puisque $ g$ est défini à une constante additive près imaginaire pure :

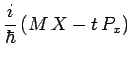$\displaystyle g(t)$ $\displaystyle =$ $\displaystyle \frac{i}{\hbar}\,(M\,X - t\,P_x)$  

L'expression cherchée de $ G$ en résulte par itération :

$\displaystyle G(V,t)$ $\displaystyle =$ $\displaystyle e^{\frac{i}{\hbar}\,V\,(M\,X - t\,P_x)}$  

et pour une transformation quelconque de Galilée portant sur un système de plusieurs particules :

$\displaystyle G(\vec{V},t)$ $\displaystyle =$ $\displaystyle e^{\frac{i}{\hbar}\,\vec{V}.\,(M\,\vec{R} - t\,\vec{P})}$  

$ \vec{R}$ et $ \vec{P}$ désignant la position et l'impulsion du centre de masse du système.


Sous-sections
suivant monter précédent table des matières
suivant: Remarque : monter: Illustrations précédent: Illustrations   Table des matières
Arnaud Balandras 2005-04-02