Puisque l'énergie potentielle ne dépend que de ![]() , il est
indiqué d'adopter les coordonnées sphériques
, il est
indiqué d'adopter les coordonnées sphériques
![]() et nous sommes ainsi conduits à introduire
la composante radiale de l'impulsion. Tenu compte de ce que les
composantes des observables vectorielles
et nous sommes ainsi conduits à introduire
la composante radiale de l'impulsion. Tenu compte de ce que les
composantes des observables vectorielles ![]() et
et ![]() ne
commutent pas, on est amené à symétriser l'expression
classique de définition de telle sorte que :
ne
commutent pas, on est amené à symétriser l'expression
classique de définition de telle sorte que :
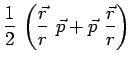 |
On remarque l'identité mathématique :
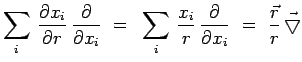 |
![]() désignant l'opérateur gradient,
d'où :
désignant l'opérateur gradient,
d'où :
De même, de la relation mathématique :
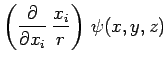 |
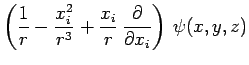 |
on en déduit la relation entre opérateurs :
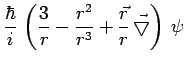 |
|||
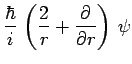 |
d'où résulte finalement :
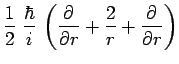 |
|||
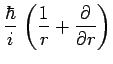 |
ou encore :
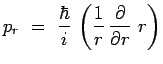 |
Question 3-31 : Montrez que :
![]() .
.
Question 3-32 : Montrez que la condition d'hermicité :
n'est satisfaite que pour des fonctions d'onde ![]() telles que :
telles que :
Question 3-33 : Déterminez les fonctions propres de ![]() et montrez que ces fonctions ne satisfont pas la condition
précédente. Qu'en déduisez-vous ?
et montrez que ces fonctions ne satisfont pas la condition
précédente. Qu'en déduisez-vous ?