 |
Un calcul purement algébrique conduit successivement aux
résultats suivants :
 |
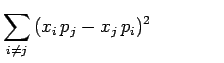 |
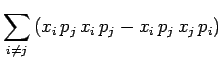 |
ou encore, tenu compte des relations de commutation :
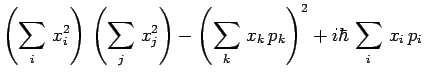 |
soit :
On remarque :
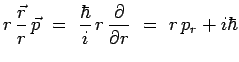 |
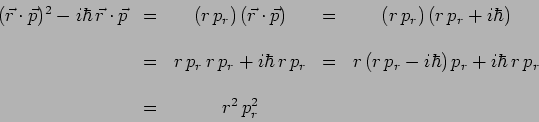 |
d'où finalement :
et donc on en déduit :
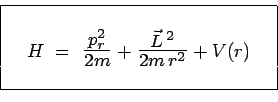 |
expression du hamiltonien valable partout
saufIII18peut-être pour ![]() . Le hamiltonien peut donc s'écrire, comme
l'énergie classique, sous la forme d'une somme de trois contributions
:
. Le hamiltonien peut donc s'écrire, comme
l'énergie classique, sous la forme d'une somme de trois contributions
:
![]() l'énergie cinétique radiale :
l'énergie cinétique radiale :
![]()
![]() l'énergie cinétique de rotation :
l'énergie cinétique de rotation :
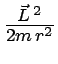
![]() l'énergie potentielle :
l'énergie potentielle : ![]()
Nous savonsIII19 que les harmoniques
sphériques sont fonctions propres communes aux observables
![]() et
et ![]() :
:
Les fonctions propres communes aux trois observables qui commutent
![]() et
et ![]() sont donc de la forme :
sont donc de la forme :
En reportant cette expression dans l'équation aux valeurs
propres de ![]() on obtient :
on obtient :
![$\displaystyle \left[ \frac{p_r^2}{2m} + \frac{l(l+1)}{2m\,r^2} + V(r)
\right]\,\Psi^m_l ~=~ E\,\Psi^m_l$](img2395.png) |
On remarque alors que la fonction radiale
![]() satisfait une équation où le nombre quantique ``
satisfait une équation où le nombre quantique ``![]() '' est
absent. Elle n'en dépend donc pas :
'' est
absent. Elle n'en dépend donc pas :
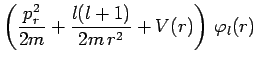 |