L'équation précédente s'appelle l'équation radiale
car c'est elle qui détermine la dépendance en ![]() , c'est-à-dire la
dépendance radiale de la fonction d'onde.
, c'est-à-dire la
dépendance radiale de la fonction d'onde.
Si dans cette équation on reporte l'expression de l'opérateur
![]() :
:
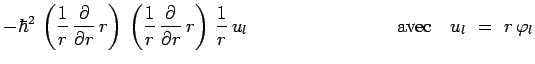 |
la fonction ![]() satisfait l'équation
différentielle du second ordre suivante :
satisfait l'équation
différentielle du second ordre suivante :
![$\displaystyle \frac{d^2{u}_l(r)}{dr^2} + \left[\varepsilon - W(r) - \frac{l(l+1)}{r^2}\right]\,u_l(r)$](img2402.png) |
0 |
après avoir posé :
 |
La solution ![]() doit être uniforme, continue et bornée
partout ainsi que sa dérivée. Donc
doit être uniforme, continue et bornée
partout ainsi que sa dérivée. Donc ![]() et sa dérivée
doivent également être uniformes, bornées et continues
partout et on doit vérifier :
et sa dérivée
doivent également être uniformes, bornées et continues
partout et on doit vérifier :
Pour une valeur de ![]() bien fixée, l'équation radiale admet en
général une infinité de solutions. A chacune de ces
solutions correspond une valeur propre
bien fixée, l'équation radiale admet en
général une infinité de solutions. A chacune de ces
solutions correspond une valeur propre
![]() et on notera
et on notera
![]() et
et
![]() les fonctions
solutions correspondantes.
les fonctions
solutions correspondantes.