h) Particule dans un puits carré

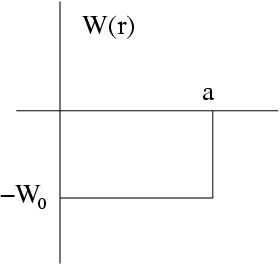
Considérons le puits de potentiel suivant : $$W(r)~=~\left\{\begin{array}{ccc} ~~0~~ & ~~~~\mathrm{si}~~~~ & r>a \\ & & \\ -W_0 & \mathrm{si} & r<a \\ \end{array}\right.$$ Dans la zone interne l'équation radiale s'écrit simplement : $$\frac{d^2{u}_l(r)}{dr^2} +\left[\varepsilon + W_0 -\frac{l(l+1)}{r^2}\right]\,u_l(r) =$$ 0

et la solution est de la forme :

$$u_l(r) = A\,r\,j_l(kr)~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{avec}~~~~~~~~~~~~~~~~~~~~~~~~k~=~\sqrt{\varepsilon+W_0}$$

Dans la zone externe $(r>a)$ l'équation est identique à celle étudiée précédemment pour la particule libre. Il y a donc lieu de distinguer les deux situations suivantes :

$\imath-$ Etats liés $\varepsilon<0$ :

La solution bornée à l'infini est de la forme :

$$B\,h_l^{(1)}(i\gamma\,r) ~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{avec}~~~~~~~~~~~~~~~~~~~~~~~~ \gamma~=~\sqrt{-\varepsilon}$$

Le raccordement au point $\,r\,=\,a\,$ des fonctions détermine le rapport $\scalebox{1.4}{$\frac{B}{A}$}$ et celui des dérivées logarithmiques :

$$\frac{1}{h_l^{(1)(i\gamma\,r)}}\, \left.\frac{d}{dr}\,h_l^{(1)}(i\gamma\,r)\,\right\vert _{\;r=a} = \left.\frac{1}{j_l(kr)}\,\frac{d}{dr}\,j_l(kr)\,\right\vert _{\;r=a}$$

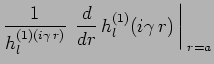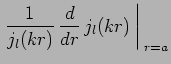détermine les seules valeurs de $\gamma$ pour lesquelles il existe une solution acceptable dans tout l'espace. L'équation ci-dessus est donc une équation de quantification de l'énergie des niveaux des états liés. Si $l=0$ cette équation se réduit à :

$$\gamma + K\,\cot Ka =$$ 0

$\imath\imath-$ Etats de diffusion $\varepsilon~=~k^2\,>\,0$ :

La solution extérieure la plus générale :

$$\Psi = A_1\;j_l(kr) + B_1\;n_l(kr)$$

est partout bornée. La continuité au point $r\;=\;a$ des fonctions et de leurs dérivées logarithmiques détermine les rapports $\frac{A_1}{A}$ et $\frac{B_1}{A}$ . Il existe une telle solution, correspondant à un état de diffusion, pour toute valeur positive de l'énergie $\varepsilon$ (continuum).