 |
Les indices 1 et 2 repèrant respectivement les observables
relatives au proton et à l'électron, le hamiltonien des deux
particules s'écrira :
 |
Si on introduit la quasi-particule associée au centre de masse,
de masse
![]() d'impulsion
d'impulsion
![]() et la quasi-particule,
associée au mouvement relatif, de masse
et la quasi-particule,
associée au mouvement relatif, de masse ![]() et d'impulsion
et d'impulsion
![]() :
:
 |
le hamiltonien prend la forme suivante :
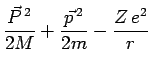 |
et admet des solutions du type :
dans laquelle l'exponentielle est une onde plane qui
décrit le mouvement rectiligne et uniforme du centre de masse,
tandis que la fonction d'onde associée au mouvement relatif est
déterminée par l'équation :
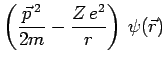 |
![]() désignant l'énergie relative, c'est-à-dire évaluée dans
le référentiel du centre de masse. Nous avons
vuIII20 que cette équation admet des
solutions particulières de la forme :
désignant l'énergie relative, c'est-à-dire évaluée dans
le référentiel du centre de masse. Nous avons
vuIII20 que cette équation admet des
solutions particulières de la forme :
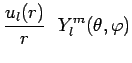 |
la fonction ![]() devant être la solution de
l'équation radiale :
devant être la solution de
l'équation radiale :
![$\displaystyle \left[ -\frac{\hbar^2}{2m}\,\frac{d^2}{dr^2} + l\,(l+1)\,\frac{\hbar^2}{2m\,r^2} -\frac{Z\,e^2}{r} - E_r\right]\,u_l(r)$](img2523.png) |
0 |
Cette équation à une seule variable ![]() est du type de celles
qui régissent les mouvements à une dimension d'une particule
et qui ont été considérées
précédemmentIII21. La condition aux
limites
est du type de celles
qui régissent les mouvements à une dimension d'une particule
et qui ont été considérées
précédemmentIII21. La condition aux
limites ![]() :
:
| 0 |
correspondant au fait que la particule ne peut pas
pénétrer dans la région non physique ![]() .
.
|
|
Par ailleurs si ![]() , le domaine de variation de
, le domaine de variation de ![]() est du
type
est du
type ![]() , tandis que pour
, tandis que pour ![]() ce domaine est du type
:
ce domaine est du type
:
Ainsi l'effet du premier terme du potentiel est de maintenir
l'électron éloigné de l'origine. D'un point de vue
classique, la force correspondant à ce terme est
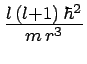 et correspond à la
force centrifuge
et correspond à la
force centrifuge
![]() puisque le moment
angulaire
puisque le moment
angulaire ![]() est tel que :
est tel que :
C'est pour cette raison que le terme correspondant s'appelle le terme centrifuge.