Il y a lieu de distinguer les solutions correspondant à des énergies positives et négatives.
![]() Si
Si ![]() :
:
La solution régulière à l'origine a un comportement oscillatoire à l'infini. Le spectre en énergie est continu et il s'agit alors d'un problème de diffusion.
![]() Si
Si ![]() :
:
Il y a intérêt à introduire les paramètres :
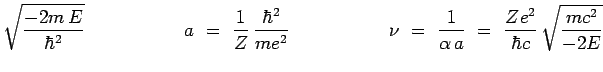 |
la nouvelle variable ![]() et la nouvelle fonction
et la nouvelle fonction
![]() définies comme suit :
définies comme suit :
L'équation radiale s'écrit alors :
![$\displaystyle \left[\rho\,\frac{d^2}{d\rho^2}+(2l+2-\rho)\,\frac{d}{d\rho}-(l+1-\nu)\right]\,y_l$](img2545.png) |
0 |
Cette équation différentielle est une équation, dite de
Laplace, dont la solution régulière à l'origine est la
série hypergéométrique confluente :
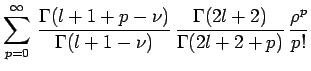 |
Cette série est en général une série infinie et se
comporte, lorsque
![]() , comme
, comme ![]() et de ce
fait ne peut donc constituer une solution normalisable et donc
acceptable. Cependant pour certaines valeurs privilégiées de
et de ce
fait ne peut donc constituer une solution normalisable et donc
acceptable. Cependant pour certaines valeurs privilégiées de
![]() les coefficients s'annulent tous à partir d'un certain
rang et la série hypergéométrique se réduit à un
polynôme. Pour que cette circonstance se produise, il faut que
les coefficients s'annulent tous à partir d'un certain
rang et la série hypergéométrique se réduit à un
polynôme. Pour que cette circonstance se produise, il faut que
![]() soit un entier négatif ou nul, soit :
soit un entier négatif ou nul, soit :
ou :
La série devient alors un polynôme de degré ![]() :
:
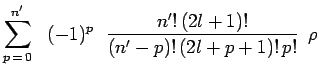 |
qui, à un facteur près, est un polynôme de
Laguerre et :