suivant monter précédent table des matières
suivant: e) Etat fondamental et monter: L'atome d'hydrogène précédent: c) Spectre d'énergie -   Table des matières

d) Fonctions propres - Nombres quantiques

A une valeur propre $ E_n$ correspond donc toutes les fonctions propres du type :

$\displaystyle \psi_{n,l,m}(r,\theta,\varphi)$ $\displaystyle =$ $\displaystyle Y^m_l(\theta,\varphi)\,\psi_{n,l}(r)$  

où $ r\,\psi_{n,l}(r)$ désigne une solution normalisée de l'équation radiale, soit explicitement :

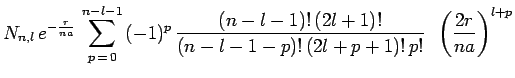$\displaystyle \psi_{n,l}(r)$ $\displaystyle =$ $\displaystyle N_{n,l}\,e^{-\frac{r}{na}}\,\sum_{p\,=\,0}^{n-l-1}\,(-1)^p\, \frac{(n-l-1)!\,(2l+1)!}{(n-l-1-p)!\,(2l+p+1)!\,p!}~\,\left(\frac{2r}{na}\right)^{l+p}$  

avec :

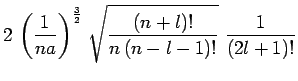$\displaystyle N_{n,l}$ $\displaystyle =$ $\displaystyle 2\,\left(\frac{1}{na}\right)^\frac{3}{2}\,\sqrt{\frac{(n+l)!}{n\,(n-l-1)!}}~\frac{1}{(2l+1)!}$  

Pour chaque énergie $ E_n$ , à laquelle correspond une valeur positive de l'entier $ n$ , on obtient l'ensemble de ces fonctions propres en donnant d'abord à $ l$ et successivement, les valeurs $ 0,1,2,\ldots$ . Pour chacune de ces valeurs de $ l$ on donne ensuite successivement à $ m$ toutes les valeurs possibles :

$\displaystyle m$ $\displaystyle =$ $\displaystyle -l~~~,~~~-l+1~~~,~~~-l+2~~~,~~~\ldots~~~,~~~0~~~,~~~1~~~,~~~2~~~,~~~\ldots~~~,~~~l$  

On dit que :

On obtient ainsi un ensemble d'états propres qu'il est commode d'associer à leur valeur propre, comme cela est indiqué sur le tableau ci-contre :

\epsffile{/home/arnaud/DossierLambert/DossierLambert/Figures/spectroscopie.eps}    
  Suivant une notation traditionnelle en spectroscopie, chaque état propre est désigné par le nombre entier positif $ n$ suivi d'une lettre caractéristique du moment angulaire et conformément à la correspondance suivante :
\begin{displaymath}\begin{array}{ccccccccc} l &=& ~~~0~~&~1~~&~2~~&~3~~&~4~~&~5~... ...\mathrm{Etat}& & s & p & d & f & g & h & \ldots \\ \end{array}\end{displaymath}      

L'ordre $ N$ de dégénérescence est indiqué dans la colonne de gauche du tableau.



suivant monter précédent table des matières
suivant: e) Etat fondamental et monter: L'atome d'hydrogène précédent: c) Spectre d'énergie -   Table des matières
Arnaud Balandras 2005-04-02