En remplaçant le paramètre ![]() par sa valeur, on obtient,
si
par sa valeur, on obtient,
si ![]() :
:
|
|
et contient un ensemble infini dénombrable de niveaux
puisque ![]() peut varier de 1 jusqu'à
peut varier de 1 jusqu'à ![]() . Lorsque
. Lorsque
![]() , ces niveaux deviennent de plus en plus
rapprochés et tendent à la limite vers la valeur
, ces niveaux deviennent de plus en plus
rapprochés et tendent à la limite vers la valeur ![]() qui
constitue un point d'accumulation, et au-delà duquel commence le
spectre continu des états de diffusion du continuum. On peut
évidemment écrire :
qui
constitue un point d'accumulation, et au-delà duquel commence le
spectre continu des états de diffusion du continuum. On peut
évidemment écrire :
de telle sorte que la différence d'énergie entre deux
niveaux est de la forme :
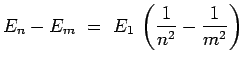 |
conformément à la théorie de Bohr. Si cette
différence d'énergie correspond à l'émission d'un photon de
fréquence ![]() :
:
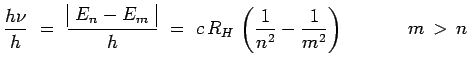 |
et la constante ![]() , dite de Rydberg, qui apparaît a
pour valeur :
, dite de Rydberg, qui apparaît a
pour valeur :
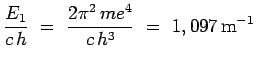 |
en complet accord avec les observations expérimentales. On retrouve bien ainsi le spectre de l'atome d'hydrogène, tel qu'il est représenté sur la figure ci-dessous :
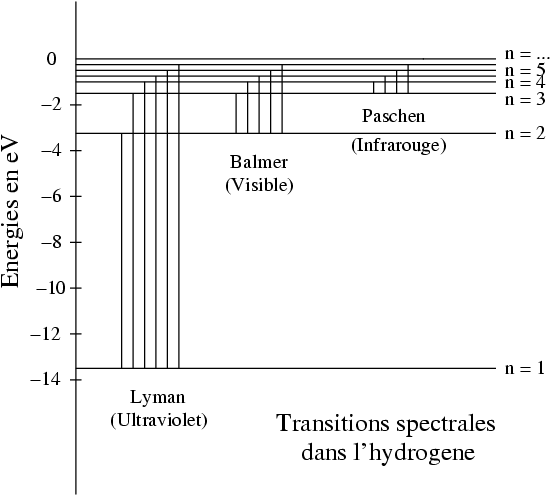
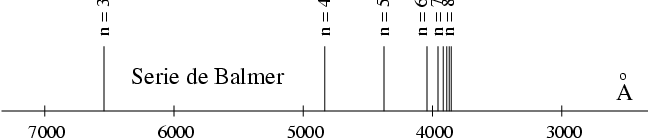
Ce spectre d'énergie est dégénéré puisque chaque énergie
quantifiée ne dépend que de ![]() , c'est-à-dire de la somme :
, c'est-à-dire de la somme :
dont chaque valeur supérieure à 1 peut être
obtenue en donnant au couple
![]() plusieurs systèmes de
valeur elles-mêmes entières et non négatives. Plus
précisément, pour chaque énergie
plusieurs systèmes de
valeur elles-mêmes entières et non négatives. Plus
précisément, pour chaque énergie ![]() , c'est-à-dire pour chaque valeur
de l'entier
, c'est-à-dire pour chaque valeur
de l'entier ![]() , le moment cinétique
, le moment cinétique ![]() peut prendre toutes les
valeurs entières depuis 0
jusqu'à
peut prendre toutes les
valeurs entières depuis 0
jusqu'à ![]() . La
dégénérescence du niveau
. La
dégénérescence du niveau ![]() est donc :
est donc :
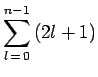 |