Prévoir c'est, par la pensée, se déplacer dans le temps, et venir se placer dans le futur. Un tel déplacement dans le temps présente une certaine analogie avec les déplacements dans l'espace, et cette analogie formelle va, ci-après, être renforcée grâce à la théorie de la relativité.
Effectuer une translation dans l'espace (définie par un vecteur
![]() ) c'est amener au point
) c'est amener au point
![]() la situation physique qui étatit
réalisée, avant déplacement au point
la situation physique qui étatit
réalisée, avant déplacement au point
![]() , de telle
sorte que la fonction d'onde, après déplacement
, de telle
sorte que la fonction d'onde, après déplacement ![]() se déduise de la
fonction d'onde
se déduise de la
fonction d'onde ![]() avant déplacement, à l'aide d'un opérateur de
déplacement induit
avant déplacement, à l'aide d'un opérateur de
déplacement induit
![]() tel que :
tel que :
avec :
De même, effectuer une translation dans le temps (définie par une durée
![]() ) c'est faire réaliser à l'instant
) c'est faire réaliser à l'instant ![]() , la situation physique qui avait
été réalisée à l'instant
, la situation physique qui avait
été réalisée à l'instant
![]() . C'est restaurer
. C'est restaurer
![]() :
:
![]() désignant l'opérateur de
déplacement dans le temps, analogue à l'opérateur
désignant l'opérateur de
déplacement dans le temps, analogue à l'opérateur
![]() de déplacement dans l'espace.
de déplacement dans l'espace.
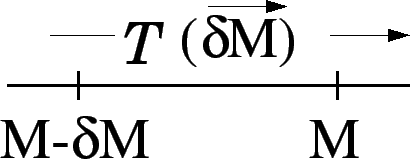
|
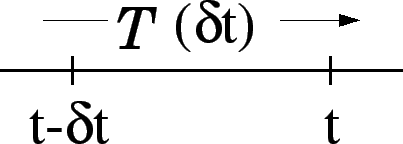
|
Les translations infinitésimales s'écrivent de manière analogue :
![]() désignant le générateur infinitésimal de translation
temporelle, et qu'il s'agit de déterminer. Pour cela, nous allons utiliser le
lien que la théorie de la relativité introduit entre les coordonnées
d'espace
désignant le générateur infinitésimal de translation
temporelle, et qu'il s'agit de déterminer. Pour cela, nous allons utiliser le
lien que la théorie de la relativité introduit entre les coordonnées
d'espace
![]() et la coordonnée temporelle, qu'il est commode
d'introduire sous la forme
et la coordonnée temporelle, qu'il est commode
d'introduire sous la forme ![]() .
.
Les trois relations démontrées précédemment :
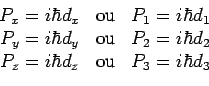 |
peuvent alors être étendues aux quatrièmes composantes :
Nous savons que
![]() désignent ici les composantes de
l'impulsion totale du système.
désignent ici les composantes de
l'impulsion totale du système. ![]() est donc la quatrième composante du
quadri-vecteur impulsion-énergie totale du système et a pour expression :
est donc la quatrième composante du
quadri-vecteur impulsion-énergie totale du système et a pour expression :
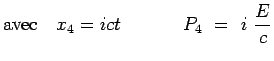 |
![]() désignant l'énergie totale du système, représentée en mécanique quantique
par un opérateur noté
désignant l'énergie totale du système, représentée en mécanique quantique
par un opérateur noté ![]() et appelé l'hamiltonien du système, de
telle sorte que :
et appelé l'hamiltonien du système, de
telle sorte que :
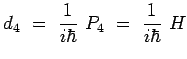 |
L'opérateur de translation infinitésimale dans le temps peut alors
s'écrire :
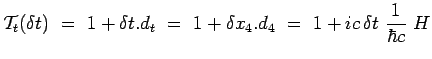 |
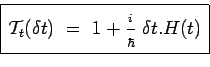 |
On notera que ![]() peut éventuellement dépendre du temps, si la fonction
classique de Hamilton dépend elle-même du temps. On découvre ainsi, que le
générateur des translations temporelles est l'opérateur hamiltonien, c'est-à-dire
l'observable énergie totale du système.
peut éventuellement dépendre du temps, si la fonction
classique de Hamilton dépend elle-même du temps. On découvre ainsi, que le
générateur des translations temporelles est l'opérateur hamiltonien, c'est-à-dire
l'observable énergie totale du système.
Question 4-1 : En comparant les opérateurs de translation induite dans l'espace et dans le temps, montrez que le formalisme quantique empêche la particule d'avoir une trajectoire.