L'expression explicite de l'opérateur 
, qui figure au second membre de
l'équation d'évolu-tion, peut s'obtenir en remplaçant dans l'expression
classique de l'énergie totale, chacune des grandeurs physiques qui y figure par
l'observable correspondante. Par exemple, dans le cas particulier d'une
particule de masse 
plongée dans un champ de forces, qui dérive de la
fonction potentielle
:
 |
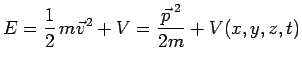l'hamiltonien s'écrit alors :
 |
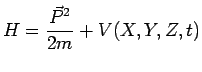L'équation d'évolution ainsi obtenue s'appelle l'équation de Schrödinger :
![$\displaystyle i\hbar~\,{{d}\over{dt}}\,\mid \Psi(t)>=
\left[{{\vec{P}^2}\over{2m}}+V(X,Y,Z,t)\right]\,\mid \Psi(t)>$](img2712.png) |
qui s'écrit encore plus explicitement dans la représentation de
Schrödinger :
![\begin{displaymath}\begin{array}{\vert ccc\vert}
\hline
& & \\
~& i\hbar~\,{{\p...
...y,z,t)\right]\,\Psi(x,y,z,t) & ~ \\
& & \\
\hline
\end{array}\end{displaymath}](img2713.png) |
On notera que la dérivée par rapport au temps est devenue une dérivée
partielle, en même temps que la fonction d'onde dépendant des variables
spatiales 
devenait également fonction du temps.