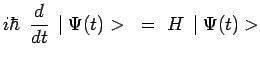 |
L'équation générale d'évolution a été établie ci-dessus, en tirant
partie des symétries entre les variables d'espace et de temps, révélées
par la théorie de la relativité. Il ne faut donc pas s'étonner, si
l'équation obtenue :
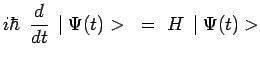 |
est potentiellement relativiste. Elle l'est effectivement (c'est-à-dire
invariante dans les transformations de Lorentz) si on remplace ![]() par une
expression relativiste de l'énergie du système étudié. Pour une particule, cette
expression dépend de la valeur de son spin.
par une
expression relativiste de l'énergie du système étudié. Pour une particule, cette
expression dépend de la valeur de son spin.
Par exemple, si
![]() (c'est le cas de l'électron en particulier),
Dirac a postulé que l'énergie était une fonction linéaire de l'impulsion
(c'est le cas de l'électron en particulier),
Dirac a postulé que l'énergie était une fonction linéaire de l'impulsion
![]() et de la masse
et de la masse ![]() :
:
![]() et
et ![]() désignant des constantes, telles que :
désignant des constantes, telles que :
identité relativiste, qui ne peut être satisfaite que si
![]() et
et ![]() désignent quatre matrices
désignent quatre matrices ![]() . L'équation ainsi obtenue :
. L'équation ainsi obtenue :
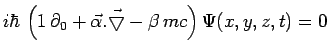 |
s'appelle l'équation de Dirac. Les matrices
![]() et
et
![]() ne peuvent agir que sur des fonctions d'onde
ne peuvent agir que sur des fonctions d'onde
![]() ayant
quatre composantes (vecteurs colonnes). Les deux premières sont celles du
spineur
ayant
quatre composantes (vecteurs colonnes). Les deux premières sont celles du
spineur
![]() de la particule (l'électron par exemple). Les
deux dernières sont celles d'un second spineur
de la particule (l'électron par exemple). Les
deux dernières sont celles d'un second spineur
![]() qui décrit
l'anti-particule qui lui est nécessairement associée
(l'anti-électron ou positron).
qui décrit
l'anti-particule qui lui est nécessairement associée
(l'anti-électron ou positron).