Opérateur d'évolution

suivant: Remarque monter: L'équation de Schrödinger précédent: Remarque 3 Table des matières

Opérateur d'évolution

Toute évolution temporelle d'un système, durant un intervalle de temps fini : $\Delta t=t-t_0$ , peut être décomposée en une succession de évolutions (avec ) durant les intervalles de temps partiels :

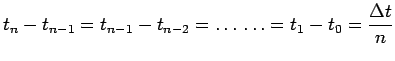$\displaystyle t_{n}-t_{n-1}=t_{n-1}-t_{n-2}=\ldots\,\ldots=t_{1}-t_{0}={{\Delta t}\over{n}}$

de telle sorte que :

$\displaystyle \mathcal{U}(t-t_0)=\mathcal{U}(t_n-t_{n-1}).\,\mathcal{U}(t_{n-1}-t_{n-2}) \ldots\,\ldots\,\mathcal{U}(t_1-t_0)$

et quand $n\rightarrow\infty$ :

$\displaystyle \mathcal{U}(t-t_0)=\lim\limits_{n\rightarrow\infty}\left[1-{{i}\o... ...t]\ldots\,\ldots \left[1-{{i}\over{\hbar}}\,{{\Delta t}\over{n}}\,H(t_1)\right]$

et si l'expression mathématique du hamiltonien ne dépend pas du temps :

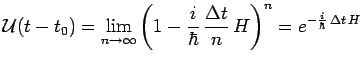$\displaystyle \mathcal{U}(t-t_0)=\lim\limits_{n\rightarrow\infty} \left(1-{{i}\... ...hbar}}\,{{\Delta t}\over{n}}\,H\right)^n= e^{-{{i}\over{\hbar}}\,{\Delta t}\,H}$

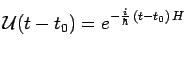
$\mathcal{U}(t-t_0)= e^{\strut-{{i}\over{\hbar}}\,(t-t_0)\,H}\strut$

Cette même équation peut également être obtenue à partir de l'équation d'évolution :

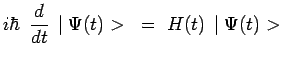$\displaystyle i\hbar~\,{{d}\over{dt}}\,\mid \Psi(t)>~=~H(t)\,\mid \Psi(t)>$

qui s'écrit encore :

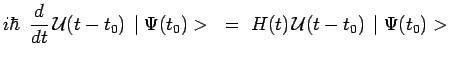$\displaystyle i\hbar~\,{{d}\over{dt}}\,\mathcal{U}(t-t_0)\,\mid \Psi(t_0)>~=~ H(t)\,\mathcal{U}(t-t_0)\,\mid \Psi(t_0)>$

quel que soit $\mid \Psi(t_0)>$ , de telle sorte que :

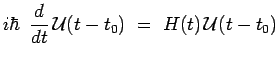$\displaystyle i\hbar~\,{{d}\over{dt}}\,\mathcal{U}(t-t_0)~=~ H(t)\,\mathcal{U}(t-t_0)$

Cette équation s'intègre, et conduit à :

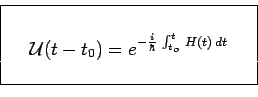$\begin{displaymath}\begin{array}{\vert ccc\vert} \hline & & \\ ~ & \mathcal{U}(... ...int_{t_o}^t\,H(t)\,dt}\strut & ~ \\ & & \\ \hline \end{array}\end{displaymath}$

Si ne dépend pas du temps, on retrouve bien l'expression précédente.

Sous-sections

Remarque

suivant: Remarque monter: L'équation de Schrödinger précédent: Remarque 3 Table des matières

Arnaud Balandras 2005-04-02