A propos de la distribution classique de
BoltzmannIV3 nous avons déjà vu
comment l'état d'un système classique peut être représenté
par un point ![]() dans l'espace des phases. Si cet état est
mal connu, on peut seulement préciser avec quelle probabilité
ce point figuratif se trouve dans un élément de volume
dans l'espace des phases. Si cet état est
mal connu, on peut seulement préciser avec quelle probabilité
ce point figuratif se trouve dans un élément de volume ![]() centré sur
centré sur ![]() dans cet espace des phases :
dans cet espace des phases :
avec :
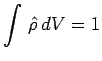 |
![]() définit une fonction densité de
probabilitéIV4 dans l'espace des phases :
définit une fonction densité de
probabilitéIV4 dans l'espace des phases :
analogue à la densité locale d'un fluide qui remplirait cet espace
des phases, la masse totale, ou la probabilité totale dans cet espace,
étant constante (et égale à 1 par exemple). Puisqu'il y a conservation de
la probabilité totale :
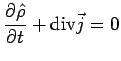 |
![]() désignant le vecteur flux dans l'espace des
phases.
désignant le vecteur flux dans l'espace des
phases.
Or une conséquence importante des équations de Hamilton, à savoir :
 |
![]() désignant la fonction énergie de Hamilton, est
que le vecteur vitesse du point
désignant la fonction énergie de Hamilton, est
que le vecteur vitesse du point ![]() dans l'espace des phases est à
divergence nulle. En effet :
dans l'espace des phases est à
divergence nulle. En effet :
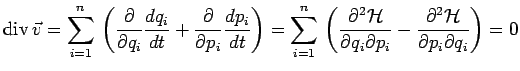 |
On en déduit immédiatement :
et :
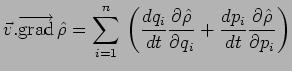 |
soit :
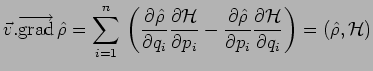 |
![]() désignant le crochet de Poisson, de
telle sorte que finalement on obtient :
désignant le crochet de Poisson, de
telle sorte que finalement on obtient :
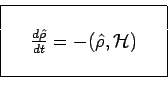 |
On notera l'analogie avec le résultat quantique que l'on aurait pu déduire directement, en utilisant la méthode de quantification de DiracIV5.
Question 4-2 : Montrez que si ![]() désigne une variable dynamique
classique
désigne une variable dynamique
classique
![]() , elle satisfait l'équation d'évolution
dans l'espace des phases :
, elle satisfait l'équation d'évolution
dans l'espace des phases :
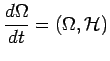 |