L'équation de Schrödinger est linéaire. Il est donc très utile d'en connaître un ensemble complet de solutions particulières, car la solution générale pourra alors s'écrire comme une combinaison linéaire quelconque de ces solutions particulières.
A cet effet, supposons résolue l'équation aux valeurs propres du hamiltonien
:
 |
désignant un paramètre de dégénérescence éventuelle.
L'état dépendant du temps :
 |
est solution de l'équation de Schrödinger. C'est un état
d'évolution possible. En effet :
 |
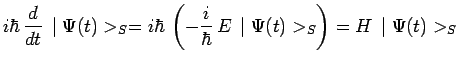puisque :
 |
Un tel état solution s'appelle un état stationnaire
(d'où l'indice inférieur 
) car, bien que le ket image
dépende du temps par son facteur exponentiel,
l'état physique lui-même est constant, puisqu'un vecteur ket et
ses multiples représente tous le même état physique. Par
construction, un tel état stationnaire est un état d'énergie
quantifiée constante. Les états d'énergie quantifiée des atomes
sont précisément de tels états. On comprend mieux maintenant
comment l'image classique des mouvements stationnaires (mouvements
immobiles !) simule la représentation quantique.
L'état général d'évolution du système pourra donc s'écrire :
 |
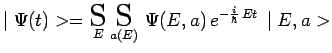