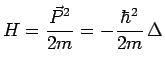Ondes planes

Considérons en particulier une particule libre ayant pour hamiltonien :

$$H={{\vec{P}^2}\over{2m}}=-{{\hbar^2}\over{2m}}\,\Delta$$

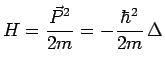Nous connaissons déjà les fonctions propres de cet hamiltonien :

$$H\,\mid \Psi_E>~=~E\,\mid \Psi_E>$$

$$\Psi_E(\vec{r})=h^{-{{3}\over{2}}}\,e^{{{i}\over{\hbar}}\,\vec{p}.\vec{r}} ~~~~~~~\mathrm{avec}~~~E={{\vec{p}^2}\over{2m}}$$

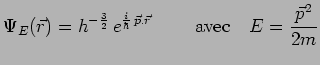On en déduit la solution particulière de l'équation de Schrödinger :

$$\Psi_E(\vec{r},t)=h^{-{{3}\over{2}}}\,e^{{{i}\over{\hbar}}\,(\vec{p}.\vec{r}-Et)} ~~~~~~~\mathrm{avec}~~~E={{\vec{p}^2}\over{2m}}$$

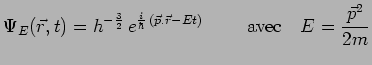Cette fonction d'onde est un état propre simultané des trois observables $P_x,P_y,P_z$ et de $H$ :

$$\begin{array}{ccccc} P_x\,\Psi_E(\vec{r},t) & = & {{\hbar}\ov... ...Psi_E(\vec{r},t) & = & E\,\Psi_E(\vec{r},t) & & \\ \end{array}$$

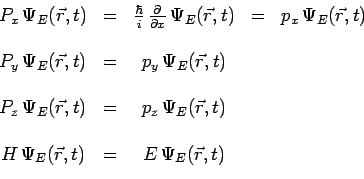Cette fonction d'onde décrit donc un état dans lequel la particule a^IV6 une impulsion $\vec{p}$ et une énergie $E$ bien définies.

Si on fait le changement de variable suivant, correspondant aux anciennes relations d'Einstein, Compton et de Broglie :

$$\vec{p}=\hbar\vec{k}~~~~~~~~~~~~~~~~~~~~~~E=\hbar\omega$$

la solution quantique s'écrit à la façon d'une onde plane classique :

$$\Psi_E(\vec{r},t)= h^{-{{3}\over{2}}}\,e^{i\,(\vec{k}.\vec{r}-\omega t)}$$

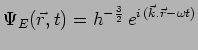qui se déplace dans l'espace physique à trois dimensions. Ici les notations ondulatoires apparaissent pour la première fois dans le formalisme quantique où $\vec{k}$ est le nombre d'ondes et $\omega$ la fréquence angulaire.