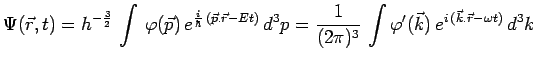 |
Puisqu'ils sont états propres de l'observable énergie, les
états ondes planes d'une particule libre constituent une
base de représentation. Par ailleurs, puisque l'équation de
Schrödinger est linéaire, toute combinaison linéaire de ces états
ondes planes sera encore solution de cette équation et
s'écrira dans la représentation de Schrödinger :
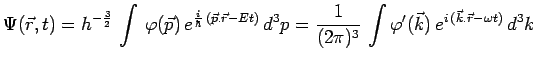 |
Question 4-3 : Démontrez que la fonction d'onde
![]() satisfait bien l'équation de Schrödinger, mais que dans cet état
satisfait bien l'équation de Schrödinger, mais que dans cet état ![]() , ni la
position, ni l'impulsion de la particule, n'ont des valeurs définies.
, ni la
position, ni l'impulsion de la particule, n'ont des valeurs définies.
La fonction d'onde ![]() est bien une somme d'ondes planes. On
l'appelle un paquet d'ondes planes. Chacune des ondes a une
vitesse de phase
est bien une somme d'ondes planes. On
l'appelle un paquet d'ondes planes. Chacune des ondes a une
vitesse de phase ![]() .
.
 |
Avec une loi de dispersion :
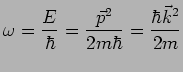 |
d'où :
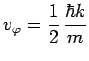 |
et une vitesse de groupe :
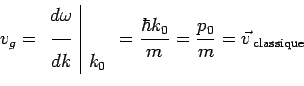 |
![]() désignant la valeur moyenne de
désignant la valeur moyenne de ![]() calculée avec la
distribution
calculée avec la
distribution
![]() .
.
Pour simplifier, mais seulement les notations, considérons un paquet d'ondes
à une dimension :
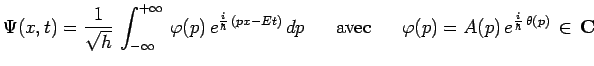 |
Supposons que la fonction ![]() soit voisine de zéro, sauf au voisinage de
soit voisine de zéro, sauf au voisinage de
![]() , et de largeur
, et de largeur ![]() . Pour que
. Pour que ![]() ait une valeur
appréciable il faut que, au voisinage de
ait une valeur
appréciable il faut que, au voisinage de ![]() et dans l'intervalle
et dans l'intervalle
![]() , la phase de l'exponentielle :
, la phase de l'exponentielle :
![$\displaystyle \Phi = \frac{1}{\hbar}\,\left[px-E(p).t+\theta(p)\right]$](img2818.png) |
varie au plus d'une quantité de l'ordre de 1 radian :
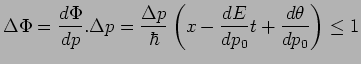 |
Cette condition est parfaitement satisfaite au point ![]() de coordonnée :
de coordonnée :
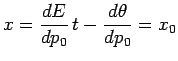 |
Ce point ![]() s'appelle le centre du paquet d'onde et se déplace en
fonction du temps avec une vitesse :
s'appelle le centre du paquet d'onde et se déplace en
fonction du temps avec une vitesse :
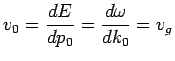 |
égale à la vitesse de groupe du paquet, elle-même égale à ce que l'on appelle la vitesse classique de la particule.
Toutefois, la condition demeure réalisée dans un voisinage ![]() du
centre
du
centre ![]() du paquet d'ondes tel que :
du paquet d'ondes tel que :
Ainsi, par un raisonnement essentiellement qualitatif, on retrouve encore l'une des relations de Heisenberg.
Problème : Etalement du paquet d'ondesIV8.