Ici encore, pour un système physique isolé dans l'espace, c'est-à-dire non soumis à des
interactions avec des champs extérieurs orientés, l'espace est
isotrope. Toutes les directions de l'espace sont équivalentes. Il n'existe
pas d'orientation absolue dans cet espace. Par suite, l'expression
mathématique classique du hamiltonien ne dépend pas de l'orientation du
repère ![]() dans l'espace. Il en résulte que l'expression quantique de ce
hamiltonien est invariante dans une rotation induite quelconque :
dans l'espace. Il en résulte que l'expression quantique de ce
hamiltonien est invariante dans une rotation induite quelconque :
et pour une rotation infinitésimale (avec
![]() ) :
) :
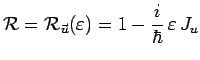 |
![]() désignant la composante dans la direction
désignant la composante dans la direction ![]() du
moment angulaire total du système :
du
moment angulaire total du système :
Quelle que soit la direction ![]() , la composante
, la composante ![]() est une constante du
mouvement, et en particulier :
est une constante du
mouvement, et en particulier :