|
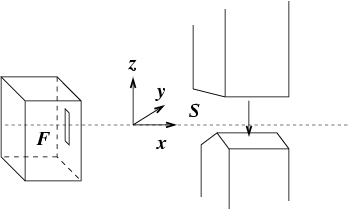
L'évolution temporelle du vecteur ket
et dont le hamiltonien a déjà été déterminéIV20: |
|
|
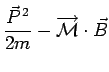 |
 |
Le champ magnétique ![]() doit satisfaire les équations de
Maxwell, en régime statique :
doit satisfaire les équations de
Maxwell, en régime statique :
dont nous choisirons la solution simple :
Si ![]() et sur la base constituée des états propres
et sur la base constituée des états propres
![]() les matrices de spin s'écriventIV21 :
les matrices de spin s'écriventIV21 :
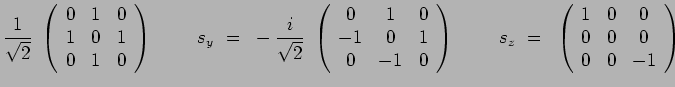 |
de telle sorte que les composantes spatiales associées
à ces états de spin :
satisfont aux équations :
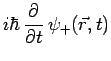 |
![$\displaystyle \frac{-\hbar^2}{2m}\,\Delta\psi_+ +
g\,\mu_B\,\left[\,\frac{-i}{\sqrt{2}}\,\alpha\,y\,\psi_0 +
(B_0-\alpha\,z)\,\psi_+\,\right]$](img3229.png) |
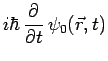 |
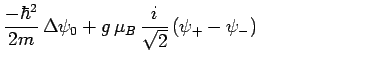 |
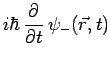 |
![$\displaystyle \frac{-\hbar^2}{2m}\,\Delta\psi_- +
g\,\mu_B\,\left[\,\frac{i}{\sqrt{2}}\,\alpha\,y\,\psi_0 -
(B_0-\alpha\,z)\,\psi_-\,\right]$](img3233.png) |
On remarque que les trois fonctions ne sont couplées entre elles
que par des termes en ![]() résultant eux-mêmes de la
contribution de
résultant eux-mêmes de la
contribution de ![]() . Or l'étudeIV22 de la
précession de Larmor révèle que, dans le cadre de
l'approximation classique, où le spin est assimilé à un
vecteur
. Or l'étudeIV22 de la
précession de Larmor révèle que, dans le cadre de
l'approximation classique, où le spin est assimilé à un
vecteur
![]() , celui-ci tourne autour du champ
magnétique
, celui-ci tourne autour du champ
magnétique ![]() avec une vitesse angulaire
avec une vitesse angulaire
![]() :
:
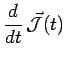 |
telle que les valeurs moyennes de ![]() et
et ![]() durant
la traversée de l'aimant sont nulles.
durant
la traversée de l'aimant sont nulles.
Il en résulte que le couplage des trois fonctions est faible.
Pour mieux le faire apparaître, il est commode d'introduire les
nouvelles fonctions :
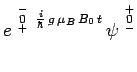 |
qui satisfont alors les équations :
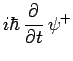 |
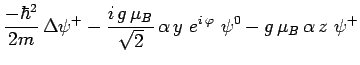 |
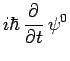 |
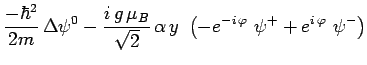 |
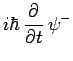 |
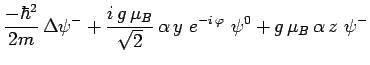 |
avec :
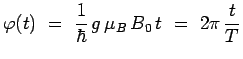 |
Durant la traversée
![]() de l'aimant (avec
de l'aimant (avec
![]() cm et
cm et
![]() m.
m.
![]() d'où
d'où
![]() s) la variation de la phase :
s) la variation de la phase :
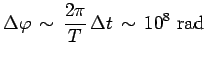 |
est si grande que durant un intervalle de temps grand
par rapport à ![]() , mais petit par rapport à
, mais petit par rapport à ![]() , la
valeur moyenne des termes de couplage en
, la
valeur moyenne des termes de couplage en ![]() est nulle, de
telle sorte que les trois équations deviennent indépendantes :
est nulle, de
telle sorte que les trois équations deviennent indépendantes :
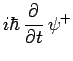 |
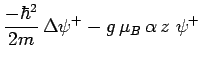 |
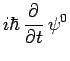 |
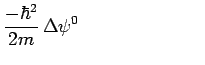 |
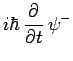 |
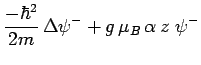 |
Les centres de ces trois paquets d'ondes se meuvent conformément
aux théorèmes d'Ehrenfest :
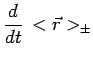 |
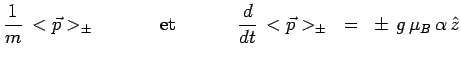 |
avec :
et donc conformément aux équations de Newton :
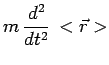 |
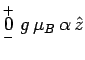 |
![]() désignant le vecteur unitaire dans la
direction du champ . Ce résultat justifie le traitement
classique du mouvement dans l'espace qui avait été pratiqué
précédemmentIV23.
désignant le vecteur unitaire dans la
direction du champ . Ce résultat justifie le traitement
classique du mouvement dans l'espace qui avait été pratiqué
précédemmentIV23.
L'état d'évolution de l'atome est donc représenté par un
vecteur ket de la forme :
Si :
et si l'intersection de ces trois régions est vide :
| 0 |
la détection de l'atome dans l'une de ces régions
provoque la réduction du paquet d'ondes et constitue une
détermination de l'état de spin et de la valeur de ![]() . Par
exemple :
. Par
exemple :
C'est cette hypothèse qui a été tacitement faite
précédemmentIV24 et qui justifie la
mesure indirecte de la composante ![]() du spin de l'atome, en le
localisant après qu'il ait traversé l'aimant de Stern et
Gerlach.
du spin de l'atome, en le
localisant après qu'il ait traversé l'aimant de Stern et
Gerlach.
En fait, les trois paquets d'ondes se chevauchent toujours mais
les recouvrements sont très faibles de telle sorte que
l'application du principe de réduction du paquet d'ondes conduit
à un état final normalisé représenté par :
et dans lequel une seule des trois composantes a des
valeurs sensibles dans la région ![]() où la particule a
été détectée, de telle sorte qu'avec une excellente
approximation le ket représentatif se réduit à l'un des
trois termes.
où la particule a
été détectée, de telle sorte qu'avec une excellente
approximation le ket représentatif se réduit à l'un des
trois termes.