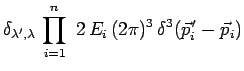 |
Avant toute chose, il s'agit de choisir une base de
représentation des états. Il est tout indiqué de choisir
pour états de base les états propres d'impulsion tant pour les
états initiaux que pour les états finalsIV30, et que l'on choisira de
normaliser comme suit :
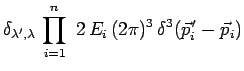 |
A ces relations d'orthonormalisation correspond la relation de
fermeture suivante :
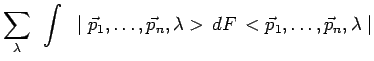 |
avec :
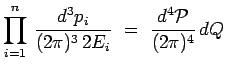 |
Cette dernière égalité correspond à un changement de
variables dans l'élément différentiel d'une intégrale
multiple, et définit notamment l'élément différentiel ![]() sachant que :
sachant que :
En effet on peut encore écrire :
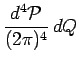 |
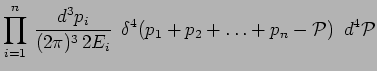 |
le signe d'égalité signifiant que les deux membres
de l'équation précédente sont équivalents quand ils
figurent tous deux sous un signe d'intégration. L'expression
explicite de l'élément différentiel ![]() en résulte
immédiatement :
en résulte
immédiatement :
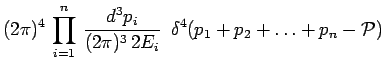 |