Vecteurs propres et coefficients de Clebsh-Gordan

Les deux ensembles de vecteurs $\mid \alpha,j_1,j_2,m_1,m_2>$ et $\mid \alpha,j_1,j_2,J,M>$ constituent deux bases standards orthonormées. Tout vecteur $\mid \alpha,j_1,j_2,J,M>$ de la nouvelle base peut donc être développé sur la base initiale :

$$\mathbf{1}=\sum\,\mid \alpha,j_1,j_2,m_1,m_2><\alpha,j_1,j_2,m_1,m_2\mid$$

$$\mid \alpha,j_1,j_2,J,M>= \sum\,\mid \alpha^\prime,j_1^\prime,j_2... ...lpha^\prime,j_1^\prime,j_2^\prime,m_1^\prime,m_2^\prime\mid \alpha,j_1,j_2,J,M>$$

et tenu compte de l'orthogonalité :

$$<\alpha^\prime,j_1^\prime,j_2^\prime,m_1^\prime,m_2^\prime\mid \a... ...,j_1^\prime}\, \delta_{j_2,j_2^\prime}\,<j_1,j_2,m_1^\prime,m_2^\prime\mid J,M>$$

on peut écrire finalement en simplifiant la notation :

$$\mid \alpha,J,M>=\sum\limits_{m_1,m_2}\,<j_1,j_2,m_1,m_2\mid J,M>\,\mid \alpha,m_1,m_2>$$

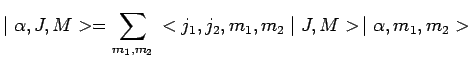On démontre que les coefficients $<j_1,j_2,m_1,m_2\mid J,M>$ , appelés coefficients de Clebsh-Gordan, sont en effet indépendants des nombres quantiques $\alpha$ . Par ailleurs, en choisissant la relation de phase suivante entre les vecteurs $\mid J,M>$ et $\mid m_1,m_2>$ pour $m_1=j_1$ et $m_2=j_2$ :

$$\begin{array}{ccc} \mid \alpha,j_1,j_2,\underbrace{j_1+j_2},\... ...~~~~~~J~~~~~~~~M & ~~~~~ & ~~~~~~~~~~m_1~~~~m_2 \\ \end{array}$$

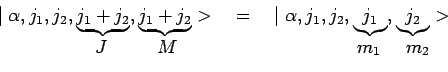On démontre que tous les coefficients de Clebsh-Gordan sont des nombres réels.

En particulier, dans le cas de l'addition de deux spins $\frac{1}{2}$ on obtient les vecteurs propres du spin total en fonction des vecteurs propres $\mid +,+>$ , $\mid +,->$ , $\mid -,+>$ et $\mid -,->$ des spins individuels. Les résultats sont indiqués dans le tableau ci-dessous :

$$\begin{array}{c\vert c\vert c} { } & S=1 & S=0 \\ & & \\ \h... ...& \\ ~~M=-1~~ & \mid 1,-1>=\mid -,-> & \\ & & \\ \end{array}$$

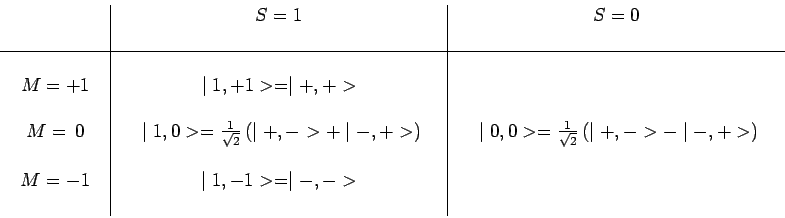On notera que les états de spin $S=1$ sont tous les trois symétriques et que l'état singulet $S=0$ est antisymétrique.