Soit enfin une troisième forme du paradoxe, due à Bohm. Considérons la
désintégration d'une particule
![]() de spin 0, en deux particules
de spin 0, en deux particules
![]() et
et
![]() toutes deux de spin
toutes deux de spin
![]() .
.
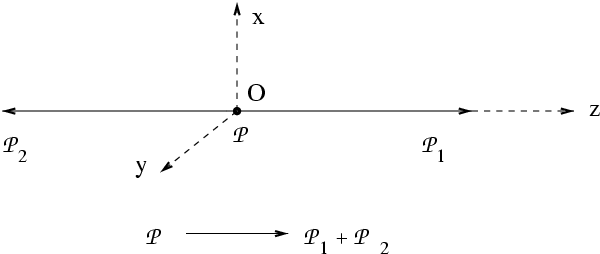
Montrons que, sans perturber en aucune manière la particule en vol
![]() , on peut en mesurer les composantes de spin
, on peut en mesurer les composantes de spin ![]() et
et ![]() le
long des deux directions
le
long des deux directions ![]() et
et ![]() perpendiculaires à la ligne
de vol
perpendiculaires à la ligne
de vol ![]() . Ici encore, il suffira pour cela de mesurer ces mêmes
composantes sur la particule associée
. Ici encore, il suffira pour cela de mesurer ces mêmes
composantes sur la particule associée
![]() .
.
L'état initial, à l'instant ![]() de la désintégration est
un état de spin total nul (
de la désintégration est
un état de spin total nul (![]() ,
, ![]() ) et ne peut être
représenté que par le vecteur ketV8 :
) et ne peut être
représenté que par le vecteur ketV8 :
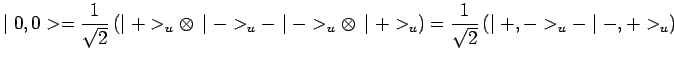 |
![]() désignant une direction quelconque (par exemple
désignant une direction quelconque (par exemple ![]() ou
ou ![]() ) de
l'espace, et :
) de
l'espace, et :
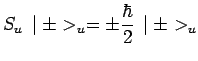 |
le premier et le deuxième ket du produit tensoriel désignant
respectivement les états de spin de la particule
![]() et de la
particule
et de la
particule
![]() .
.
Question 5-10 : Justifiez l'affirmation précédente
et l'expression du vecteur ket ![]() .
.
Nous nous proposons de prédire avec certitude et sans aucunement
agir sur la particule
![]() la valeur que l'on trouvera,
si à l'instant
la valeur que l'on trouvera,
si à l'instant ![]() on mesure la composante
on mesure la composante ![]() de son
spin. A cet effet, il suffit à l'instant
de son
spin. A cet effet, il suffit à l'instant ![]() de mesurer la
composante
de mesurer la
composante ![]() du spin de la particule
du spin de la particule
![]() . En
effet, à cet instant
. En
effet, à cet instant ![]() , l'état de spin total est encore
représenté par le même ket
, l'état de spin total est encore
représenté par le même ket ![]() .
.
Question 5-11 : Justifiez l'affirmation précédente
en montrant pourquoi l'état ![]() est un état
stationnaire de spin.
est un état
stationnaire de spin.
Selon le formalisme quantique, cette mesure de ![]() provoque à l'instant
provoque à l'instant
![]() la réduction du paquet d'ondes, et si on trouve par exemple
la réduction du paquet d'ondes, et si on trouve par exemple
![]() :
:
de telle sorte que la mesure ultérieure à l'instant ![]() de
de
![]() fournira avec certitude le résultat :
fournira avec certitude le résultat :
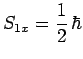 |
Si on choisit ![]() de telle sorte que
de telle sorte que ![]() est inférieur à la distance
qui sépare les deux particules à l'instant
est inférieur à la distance
qui sépare les deux particules à l'instant ![]() , on peut être assuré que
cette valeur de
, on peut être assuré que
cette valeur de ![]() n'a pas été acquise par la particule
n'a pas été acquise par la particule
![]() en conséquence d'une interaction provoquée par la mesure de
en conséquence d'une interaction provoquée par la mesure de
![]() . Puisque cette valeur de
. Puisque cette valeur de ![]() était antérieure à cette mesure
de
était antérieure à cette mesure
de ![]() , et en est donc indépendante, la particule
, et en est donc indépendante, la particule
![]() a donc
été émise dans un état de spin tel que :
a donc
été émise dans un état de spin tel que :
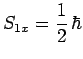 |
Question 5-12 : Justifiez l'affirmation précédente.
On montrerait de la même manière en mesurant ![]() que la particule
que la particule
![]() a été émise avec une valeur de
a été émise avec une valeur de ![]() bien définie.
bien définie.
Question 5-13 : Peut-on affirmer également que la particule
![]() a été émise avec une valeur de
a été émise avec une valeur de ![]() bien définie ?
bien définie ?
Ainsi, puisque les valeurs de ![]() et de
et de ![]() peuvent être prédites
avec certitude, et sans agir sur cette particule
peuvent être prédites
avec certitude, et sans agir sur cette particule
![]() , il résulte
du critère de réalité de Einstein que ces valeurs constituent deux
éléments de réalité physique que possède en même temps cette particule
, il résulte
du critère de réalité de Einstein que ces valeurs constituent deux
éléments de réalité physique que possède en même temps cette particule
![]() .
.
Conformément au formalisme quantique l'état physique correspondant devrait
être repré-senté par un vecteur ket qui soit en même temps état propre
de ![]() et de
et de ![]() . Or un tel vecteur ket n'existe pas.
. Or un tel vecteur ket n'existe pas.
Question 5-14 : Justifiez l'affirmation précédente et montrez que la
non commutation de ![]() et
et ![]() ne suffit pas pour cela.
ne suffit pas pour cela.
Ainsi, il existerait des états physiques de spin possèdant plus de propriétés simultanées que ne le prévoit la mécanique quantique. Ne sachant pas représenter ces états, la mécanique quantique serait donc, selon Einstein, incomplète et constituerait seulement une théorie statistique, un peu à l'image de la thermodynamique (statistique) par rapport à la mécanique de Newton, qui régit le comportement des particules constituantes du système étudié.
C'est seulement dans le chapitre VI que nous examinerons cette interprétation statistique de la mécanique quantique par Einstein, en même temps que nous examinerons les autres interprétations, et notamment celle dite de l'école de Copenhague, et comment celle-ci prétend réfuter les conclusions de Einstein.