Selon ce postulat, l'espace
![]() des vecteurs kets associé à l'ensemble
des vecteurs kets associé à l'ensemble ![]() de deux sous-systèmes physiques
de deux sous-systèmes physiques ![]() et
et ![]() , est le produit tensoriel de deux
espaces
, est le produit tensoriel de deux
espaces
![]() et
et
![]() associés à
associés à ![]() et
et ![]() :
:
Si
![]() noté
noté ![]() est un E.C.O.C. de
est un E.C.O.C. de
![]() et
et
![]() noté
noté ![]() est un E.C.O.C.
de
est un E.C.O.C.
de
![]() , l'ensemble des produits
, l'ensemble des produits
![]() formés avec les vecteurs propres
formés avec les vecteurs propres ![]() de
de ![]() (communs aux observables
(communs aux observables ![]() ) et les vecteurs propres
) et les vecteurs propres ![]() de
de ![]() (communs aux observables
(communs aux observables ![]() ) constitue une base de
représentation dans
) constitue une base de
représentation dans
![]() .
.
 |
Les vecteurs de base
![]() sont donc alors factorisables,
mais un vecteur quelconque
sont donc alors factorisables,
mais un vecteur quelconque ![]() de
de
![]() ne l'est
pas :
ne l'est
pas :
Par suite, dans l'état représenté par le ket
![]() ,
le système
,
le système ![]() est dans un état représenté par
est dans un état représenté par ![]() et
le système
et
le système ![]() est dans un état représenté par
est dans un état représenté par ![]() , et
ces deux états sont alors indépendants, comme nous
l'avons déjà remarqué précédemmentV9 :
, et
ces deux états sont alors indépendants, comme nous
l'avons déjà remarqué précédemmentV9 :
Au contraire dans un état du système global ![]() représenté par un vecteur :
représenté par un vecteur :
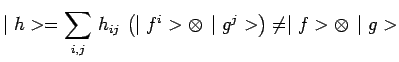 |
il n'existe aucun vecteur ket, tel que ![]() susceptible de représenter un état
susceptible de représenter un état ![]() de
de ![]() , et de même
pour
, et de même
pour ![]() de
de ![]() . Ainsi le formalisme indique que les états
individuels
. Ainsi le formalisme indique que les états
individuels ![]() et
et ![]() n'existent pas puisqu'ils ne peuvent
pas être représentésV10. Par conséquent, dans
l'état
n'existent pas puisqu'ils ne peuvent
pas être représentésV10. Par conséquent, dans
l'état ![]() de
de ![]() , ni
, ni ![]() ni
ni ![]() n'admettent d'états
individuels. On remarquera que les suites des états
n'admettent d'états
individuels. On remarquera que les suites des états ![]() pour
pour ![]() et
et ![]() pour
pour ![]() ne jouissent d'aucun statut
privilégié, puisque la décomposition de
ne jouissent d'aucun statut
privilégié, puisque la décomposition de ![]() n'est pas
unique. En effet, en adoptant un nouvel E.C.O.C. :
n'est pas
unique. En effet, en adoptant un nouvel E.C.O.C. :
![]() dans
dans
![]() et un nouvel E.C.O.C. qui est
et un nouvel E.C.O.C. qui est
![]() dans
dans
![]() on obtient :
on obtient :
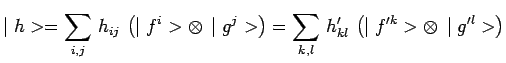 |
Ainsi l'état ![]() de
de ![]() attribue aux systèmes
attribue aux systèmes ![]() et
et ![]() des
couples d'états corrélés tels que
des
couples d'états corrélés tels que
![]() ou
ou
![]() et la
force de cette corrélation est mesurée par la valeur
des coefficients
et la
force de cette corrélation est mesurée par la valeur
des coefficients ![]() ou
ou
![]() .
.