b) Etats de particules indiscernables

Le postulat VIII (principe de Pauli) exige que la fonction d'onde d'un ensemble de $n$ fermions identiques (les électrons au sein d'un atome par exemple) soit un déterminant de Slater :

$$\Psi_A(\vec{r}_1,\vec{r}_2,\ldots,\vec{r}_n)=\frac{1}{\sqrt{n... ...a,\beta,\ldots,\omega \\ j=1,2,\ldots,n \\ \end{array}\right.$$

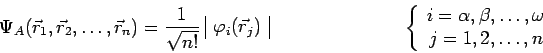ou encore en développant un tel déterminant :

$$\Psi_A(\vec{r}_1,\vec{r}_2,\ldots,\vec{r}_n)=\frac{1}{\sqrt{n!}}~... ...rphi_\alpha(\vec{r}_1).\varphi_\beta(\vec{r}_2)\ldots \varphi_\omega(\vec{r}_n)$$

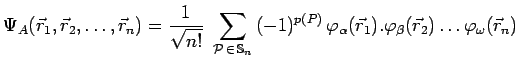La somme de produits qui figure au second membre ne peut évidemment pas s'écrire sous la forme d'un unique produit de $n$ fonctions. Par suite, l'état global du cortège électronique est un mélange inséparable des $n$ états individuels occupés. Chaque électron n'occupe pas un état ou une orbitale déterminée. On ne peut même pas affirmer que chaque électron occupe potentiellement chacun des états de la suite précédente si cette suite était définie univoquement. En effet, le déterminant de Slater est invariant si on remplace cette suite par une autre suite constituée avec des combinaisons linéaires et indépendantes $\varphi_i^\prime(\vec{r})$ des $n$ précédents états individuels occupés :

$$\varphi_i(\vec{r})~~\longrightarrow~~\varphi_i^\prime(\vec{r})= \sum\limits_j\,M_{ij}\,\varphi_j(\vec{r})$$

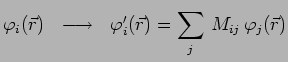Question 5-16 : Justifiez l'affirmation précédente, et précisez les contraintes éventuelles auxquelles doit satisfaire la matrice $(M_{ij})$ .

Ainsi, le vecteur ket $\mid \Psi>$ bien défini qui représente l'état global du cortège électronique, n'est pas défini par une suite précise et unique de vecteurs kets $\mid \alpha>,\mid \beta>,\ldots,\mid \omega>$ représentant des états individuels occupés. Une infinité de telles suites $\mid \alpha^\prime>,\mid \beta^\prime>,\ldots,\mid \omega^\prime>$ peuvent convenir. Ce qui caractérise le ket $\mid \Psi>$ , c'est l'espace des états occupés, engendré par l'une quelconque de ces suites, et les corrélations entre les états occupés de cette suite. Le cortège électronique constitue donc un tout inséparable de $n$ électrons indiscernables.