Considérons à nouveau l'ensemble ![]() des deux sous-systèmes physiques
des deux sous-systèmes physiques ![]() et
et ![]() ,
dans un état quelconque représenté par le vecteur ket déjà défini
précédemment :
,
dans un état quelconque représenté par le vecteur ket déjà défini
précédemment :
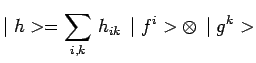 |
Par exemple, ![]() et
et ![]() pourraient désigner les deux particules de spin
pourraient désigner les deux particules de spin
![]() déjà considérées dans le paradoxe E.P.R., et résultant
de la désintégration d'une particule
déjà considérées dans le paradoxe E.P.R., et résultant
de la désintégration d'une particule ![]() de spin zéro :
de spin zéro :
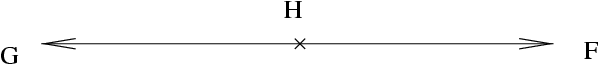
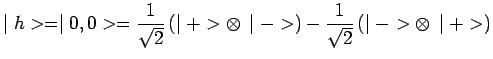 |
Comme nous l'avons déjà remarqué, toute mesure effectuée sur la
particule ![]() a pour effet, dans le formalisme quantique, de mettre
instantanément la particule
a pour effet, dans le formalisme quantique, de mettre
instantanément la particule ![]() dans un état déterminé, et ceci quelle
que soit la distance qui sépare les deux particules. On pourrait alors penser
que cet effet pourrait permettre de transmettre instantanément des signaux à
grande distance, ce qui constituerait une violation du principe de relativité
de Einstein. Nous allons montrer d'une façon générale, qu'il n'en est
rien.
dans un état déterminé, et ceci quelle
que soit la distance qui sépare les deux particules. On pourrait alors penser
que cet effet pourrait permettre de transmettre instantanément des signaux à
grande distance, ce qui constituerait une violation du principe de relativité
de Einstein. Nous allons montrer d'une façon générale, qu'il n'en est
rien.
Supposons donc que des mesures soient (ou ne soient pas) effectuées sur le système (ou la particule). Nous allons montrer que ces mesures éventuelles et leurs résultats sont sans effet sur les observations effectives faites sur le système.
En effet, si ![]() désigne une observable quelconque mesurée sur le système
désigne une observable quelconque mesurée sur le système
![]() , il suffit de connaitre l'opérateur densité
, il suffit de connaitre l'opérateur densité ![]() des états de
des états de ![]() ,
pour prédire tous ces résultats de mesure :
,
pour prédire tous ces résultats de mesure :
Il suffit donc de calculer ![]() et de démontrer qu'il est indépendant
des mesures éventuelles effectuées sur
et de démontrer qu'il est indépendant
des mesures éventuelles effectuées sur ![]() .
.
A cet effet, calculons la valeur moyenne de ![]() mesurée dans
l'état
mesurée dans
l'état ![]() du système global :
du système global :
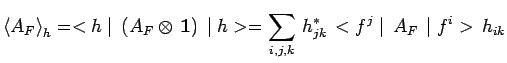 |
soit :
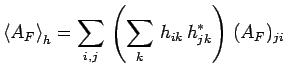 |
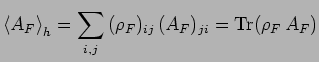 |
avec :
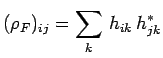 |
ou :
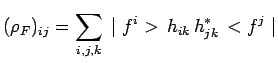 |
![]() est l'opérateur densité de
est l'opérateur densité de ![]() quand aucune mesure n'est
effectuée sur
quand aucune mesure n'est
effectuée sur ![]() .
.
Supposons maintenant que sur ![]() on effectue la mesure d'une
observable, ou même d'un E.C.O.C. Il est alors commode de
choisir cet E.C.O.C. pour E.C.O.C. de base, dont les vecteurs
propres
on effectue la mesure d'une
observable, ou même d'un E.C.O.C. Il est alors commode de
choisir cet E.C.O.C. pour E.C.O.C. de base, dont les vecteurs
propres ![]() constituent précisément la base déjà
choisie dans
constituent précisément la base déjà
choisie dans
![]() .
.
On sait déjà que si on trouve pour résultat de mesure
![]() , une
application directe du postulat IV de réduction du paquet d'ondes indique que
la particule
, une
application directe du postulat IV de réduction du paquet d'ondes indique que
la particule ![]() doit être représentée par le ket normalisé :
doit être représentée par le ket normalisé :
 |
La probabilité d'être placée dans cet état est égale à
la probabilité de trouver le résultat de mesure ![]() , soit en
rappelant l'expression générale de cette
probabilitéV13 :
, soit en
rappelant l'expression générale de cette
probabilitéV13 :
et dans le cas particulier suivant :
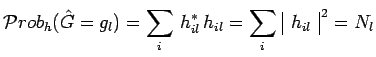 |
On en déduit l'expression de l'opérateur densité ![]() du
système
du
système ![]() en utilisant l'expression générale d'un opérateur
densitéV14 :
en utilisant l'expression générale d'un opérateur
densitéV14 :
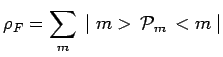 |
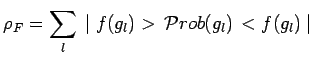 |
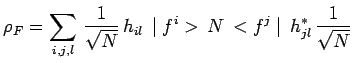 |
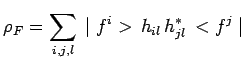 |
On retrouve bien la même expression que précédemment.
Ainsi le fait d'effectuer (ou de ne pas effectuer) les mesures de telles ou
telles observables sur le système ![]() est sans effet sur les observations sur le
système
est sans effet sur les observations sur le
système ![]() . On pourrait peut-être encore penser que l'on pourrait faire usage
des résultats de mesure de
. On pourrait peut-être encore penser que l'on pourrait faire usage
des résultats de mesure de ![]() eux-mêmes, pour agir sur les
observations faites sur
eux-mêmes, pour agir sur les
observations faites sur ![]() . Ce serait oublier que les résultats de mesure
sont aléatoires.
. Ce serait oublier que les résultats de mesure
sont aléatoires.
En effet, par exemple, en utilisant le dispositif E.P.R., on sait que si :
 |
mais pour transmettre un message, il faudrait que ![]() puisse
choisir à volonté ses résultats de mesure successifs :
puisse
choisir à volonté ses résultats de mesure successifs :
![]() etc, ce qu'il ne peut pas faire. Toutefois il est vrai que les deux observateurs
peuvent par exemple s'accorder préalablement pour déclencher chacun un
mécanisme (une horloge par exemple) quand ils obtiendront l'un et l'autre les
résultats de mesure indiqués ci-dessus. Un tel signal part indifféremment
de
etc, ce qu'il ne peut pas faire. Toutefois il est vrai que les deux observateurs
peuvent par exemple s'accorder préalablement pour déclencher chacun un
mécanisme (une horloge par exemple) quand ils obtiendront l'un et l'autre les
résultats de mesure indiqués ci-dessus. Un tel signal part indifféremment
de ![]() ou de
ou de ![]() et ne constitue pas un échange d'information. Un éclair
lumineux émis à mi-distance de
et ne constitue pas un échange d'information. Un éclair
lumineux émis à mi-distance de ![]() et
et ![]() ferait aussi bien l'affaire pour
synchroniser les deux horloges et cette méthode de synchronisation est bien
évidemment compatible avec la relativité.
ferait aussi bien l'affaire pour
synchroniser les deux horloges et cette méthode de synchronisation est bien
évidemment compatible avec la relativité.