L'optique ondulatoire obéit au principe de Huygens qui, par
exemple, permet de détermi-ner la grandeur du champ
électromagnétique créé en un point ![]() , par la lumière
issue d'une source
, par la lumière
issue d'une source ![]() après traversée d'un trou percé dans
un écran.
après traversée d'un trou percé dans
un écran.
|
|
Chaque point ![]() est alors considéré comme une source
intermédiaire qui produit au point
est alors considéré comme une source
intermédiaire qui produit au point ![]() un champ de grandeur :
un champ de grandeur :
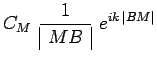 |
les constantes ![]() et
et ![]() ne dépendant que de
l'intensité de la source
ne dépendant que de
l'intensité de la source ![]() .
.
Le principe de Huygens, encore appelé principe des sources
indépendantes, permet alors de calculer directement l'amplitude
du champ créé par la source ![]() au point
au point ![]() :
:
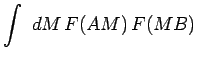 |
|||
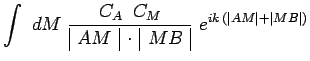 |
l'intégrale étant étendue à tous les points ![]() de la surface du trou. L'intensité lumineuse au point
de la surface du trou. L'intensité lumineuse au point ![]() s'en
déduit :
s'en
déduit :
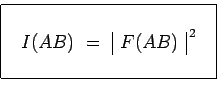 |
|
|
Le principe de Huygens postule que l'amplitude du champ créé
en un point ![]() par la source
par la source ![]() peut s'écrire :
peut s'écrire :
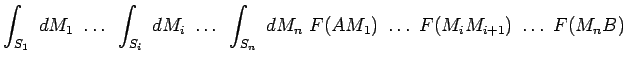 |
En considérant des surfaces ![]() de plus en plus voisines, on
peut définir un nombre d'onde local en chaque point
de plus en plus voisines, on
peut définir un nombre d'onde local en chaque point ![]() de
telle sorte qu'en introduisant la fréquence
de
telle sorte qu'en introduisant la fréquence
![]() de la lumière qui est une quantité
indépendante du milieu :
de la lumière qui est une quantité
indépendante du milieu :
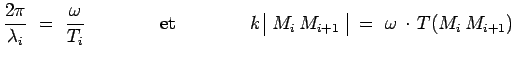 |
![]() désignant la durée du trajet
désignant la durée du trajet
![]() de telle sorte que finalement :
de telle sorte que finalement :
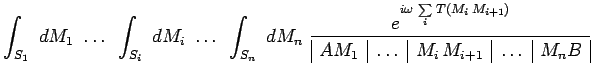 |
L'intensité créée au point ![]() par la source
par la source ![]() peut enfin
s'écrire symboliquement :
peut enfin
s'écrire symboliquement :
Dans l'intégrale, tous les chemins possibles contribuent
à la grandeur du champ au point ![]() par un terme de module
unité et dont la phase est l'intégrale de temps
calculée classiquement pour chacun de ces chemins possibles.
par un terme de module
unité et dont la phase est l'intégrale de temps
calculée classiquement pour chacun de ces chemins possibles.