A chaque instant ![]() l'état d'un système classique quelconque peut
être caractérisé par les valeurs prises à cet instant par
un nombre minimum
l'état d'un système classique quelconque peut
être caractérisé par les valeurs prises à cet instant par
un nombre minimum ![]() de paramètres indépendants
de paramètres indépendants ![]() fonctions du temps. Ce nombre
fonctions du temps. Ce nombre ![]() s'appelle le nombre de
degrés de liberté de ce système.
s'appelle le nombre de
degrés de liberté de ce système.
A ce système on peut associer une fonction caractéristique de ce
système appelée sa fonction de Lagrange ![]() , elle-même
fonction des fonctions
, elle-même
fonction des fonctions ![]() et
et
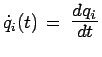 et éventuellement du
temps.
et éventuellement du
temps.
Classiquement, cette fonction ![]() est la différence entre la
fonction énergie cinétique
est la différence entre la
fonction énergie cinétique ![]() et la fonction énergie potentielle
et la fonction énergie potentielle ![]() :
:
L'état initial ![]() et l'état final
et l'état final ![]() étant
supposés connus, toute évolution
étant
supposés connus, toute évolution ![]() possible qui puisse
connecter ces deux états est déterminée par des fonctions
possible qui puisse
connecter ces deux états est déterminée par des fonctions
![]() telles que :
telles que :
Ces fonctions ![]() peuvent être considérées comme
étant les coordonnées d'un point mobile
peuvent être considérées comme
étant les coordonnées d'un point mobile ![]() qui décrit un
chemin
qui décrit un
chemin ![]() dans un espace mathématique à
dans un espace mathématique à ![]() dimensions
appelé espace de configuration. A tout chemin
dimensions
appelé espace de configuration. A tout chemin ![]() correspond une valeur prise sur ce chemin par l'intégrale
d'action
correspond une valeur prise sur ce chemin par l'intégrale
d'action
![]() :
:
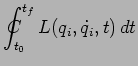 |
Le principe de moindre action affirme que le bon chemin ![]() ,
c'est-à-dire celui qui correspond à l'évolution effective du système
; c'est-à-dire celui qui est conforme aux lois de la mécanique :
,
c'est-à-dire celui qui correspond à l'évolution effective du système
; c'est-à-dire celui qui est conforme aux lois de la mécanique :
est celui pour lequel l'intégrale
![]() prend sa valeur minimum de telle sorte que, pour toute variation :
prend sa valeur minimum de telle sorte que, pour toute variation :
considérée au voisinage de ce chemin ![]() , le
terme de premier ordre
, le
terme de premier ordre
![]() dans la variation
de l'action est nul :
dans la variation
de l'action est nul :
![$\displaystyle \delta^{(1)}\,\left[\int_{t_1}^{t_2}\hspace{-.70cm}C\hspace{.30cm...
...mathcal{S}(\hat{q}_i + \delta q_i) - \mathcal{S}(\hat{q}_i)~\right]^{(1)} ~=~ 0$](img4063.png) |
Grâce à ce principe de moindre action, déterminer
l'évolution temporelle effective du système physique considéré
revient à déterminer les fonctions
![]() qui ont pour
effet de rendre minimum la valeur de l'intégrale d'action
qui ont pour
effet de rendre minimum la valeur de l'intégrale d'action
![]() .
.
Considérons en particulier l'évolution d'une particule
classique soumise à des forces qui dérivent d'une fonction
potentielle ![]() indépendante du temps, de telle sorte que :
indépendante du temps, de telle sorte que :
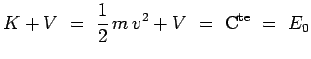 |
l'intégrale d'action calculée entre la position
initiale de la particule
![]() et sa position finale
et sa position finale
![]() s'écrit :
s'écrit :
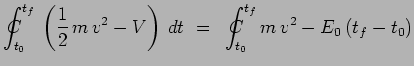 |
et avec
![]() on obtient :
on obtient :
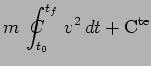 |
de telle sorte que le principe de moindre action
s'écrit encore :
![$\displaystyle \delta^{(1)}\,\left[~\int_{M_0}^{M_f}\hspace{-.90cm}C\hspace{.50cm}\,v\,d\ell~\right] ~=~ 0$](img4071.png) |
Cette dernière expression est celle du principe de Maupertuis. On notera la grande analogie entre l'expression mathématique du principe de Fermat et celle du principe de Maupertuis :
| Fermat | Maupertuis | ||||||||||
|
|
Cette analogie devient encore plus remarquable si on rappelle la
relation de de Broglie entre la vitesse de phase ![]() d'une onde et
la vitesse de groupe
d'une onde et
la vitesse de groupe ![]() qui est la vitesse de la particule
associée :
qui est la vitesse de la particule
associée :