Le Postulat III de Born

Le postulat III donne au formalisme de la mécanique quantique sa signification opération-nelle. Il permet de répondre à la question fondamentale suivante : connaissant l'état dans lequel se trouve un système physique et sur lequel on se propose de mesurer une certaine grandeur $\hat{A}$ , quel sera le résultat de cette mesure ?

Pour simplifier d'abord l'aspect mathématique, nous supposerons que l'observable $A$ qui représente la grandeur mesurée admet un spectre discret et non dégénéré, auquel est associé une base orthonormée bien définie de vecteurs propres $\{\mid a_i>\}$ :

$$A\mid a_i>=a_i\mid a_i>$$

avec $<a_i\mid a_j>=\delta_{ij}~~~(i,j=1,2,\ldots,n,\ldots\infty)$ .

Le principe de Born s'énonce alors comme suit :

POSTULAT III

Si, sur un système physique dans un état $\Psi$ représenté par le vecteur ket normé $\mid \Psi>\in$ $\cal{H}_{\cal{S}}$ avec $<\Psi\mid \Psi>=1$ , on mesure une grandeur physique $\hat{A}$ représentée par l'observable $A$ , dont les valeurs propres $a_i$ sont discrètes et non dégénérées, et dont les vecteurs propres $\mid a_i>$ sont normés, $<a_i\mid a_i>=1$ , alors :

$\imath-$ le résultat de mesure sera l'une quelconque $a_i$ des valeurs propres de l'observable $A$ .

$\imath\imath-$ si cette mesure est répétée un très grand nombre de fois, la probabilité de trouver $a_k$ pour résultat de mesure est égale à :

$$\mathcal{P}_k=\mathcal{P}(\hat{A}=a_k)=\mid <a_k\mid \Psi>\mid ^2=\mid \Psi_k\mid ^2$$

Ce principe s'appelle aussi principe de décomposition spectrale, en raison du fait que pour obtenir immédiatement toutes les probabilités $\mathcal{P}_k$ , il faut décomposer le ket $\mid \Psi>$ sur la base constituée de tous les états propres $\mid a_i>$ associés à toutes les valeurs propres $a_i$ du spectre de l'observable $A$ mesurée :

$$\mid \Psi>={\mathbf 1}\,\mid \Psi>=\sum\limits_{i=1}^\infty~\mid a_i><a_i\mid \Psi>$$

$$\mid \Psi>=\Psi_1\mid a_1>+\Psi_2\mid a_2>+\ldots+\Psi_k\mid a_k>+\ldots$$

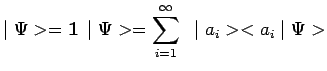Si, au lieu de mesurer la variable dynamique $\hat{A}$ , on mesure une autre variable dynamique $\hat{B}$ , représentée par une autre observable $B$ , dont le spectre sera également supposé discret et non dégénéré ;

$$B\mid b_j>=b_j\mid b_j>$$

$$<b_i\mid b_j>=\delta_{ij}$$

la décomposition spectrale devra se faire sur la base orthonormée constituée des vecteurs propres $\mid b_j>$ de $B$ :

$$\mid \Psi>=\sum\limits_{j}~\mid b_j><b_j\mid \Psi>=\sum\limits_{j}~\Psi^\prime_j~\mid b_j>$$

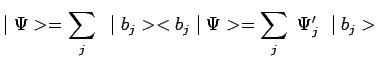Tout résultat de mesure sera l'une quelconque $b_j$ des valeurs propres de $B$ et sera obtenue avec la probabilité :

$$\mathcal{P}(\hat{B}=b_j)=\mid <b_j\mid \Psi>\mid ^2=\mid \Psi^\prime_j\mid ^2$$