Le mélange
![]() d'états propres codés
d'états propres codés ![]() ,
ainsi réalisé après mesure de la grandeur physique
,
ainsi réalisé après mesure de la grandeur physique ![]() ,
semble équivalent à l'état codé
,
semble équivalent à l'état codé ![]() sur lequel la mesure
de
sur lequel la mesure
de ![]() a été effectuée. En effet, dire que le système est
dans l'état
a été effectuée. En effet, dire que le système est
dans l'état ![]() c'est affirmer que, si la mesure de
c'est affirmer que, si la mesure de ![]() est effectuée, on trouvera le résultat
est effectuée, on trouvera le résultat
![]() avec la
probabilité
avec la
probabilité
![]() . Or, le mélange
. Or, le mélange
![]() d'états considéré est précisément la réalisation
effective de cette prédiction. Nous allons toutefois constater
que cette équivalence n'est vérifiée que pour la mesure de
d'états considéré est précisément la réalisation
effective de cette prédiction. Nous allons toutefois constater
que cette équivalence n'est vérifiée que pour la mesure de
![]() . Au contraire, toute autre mesure que celle de
. Au contraire, toute autre mesure que celle de
![]() , par exemple celle d'une autre grandeur
, par exemple celle d'une autre grandeur ![]() ,
conduira en général à des résultats différents si elle
est effectuée sur le mélange
,
conduira en général à des résultats différents si elle
est effectuée sur le mélange
![]() précédent ou
sur l'état
précédent ou
sur l'état ![]() qui lui a donné naissance.
qui lui a donné naissance.
En effet, considérons pour simplifier ici et dans la suite, le cas où les
valeurs propres sont discrètes et non dégénérées :
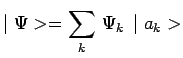 |
avec :
Si la mesure de ![]() est effectuée sur cet état
est effectuée sur cet état ![]() :
:
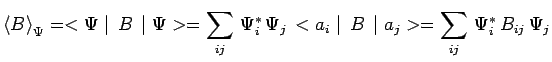 |
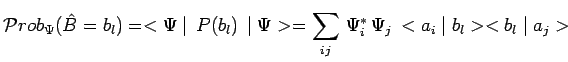 |
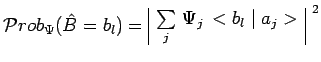 |
Au contraire si cette même mesure de ![]() est effectuée
sur le mélange
est effectuée
sur le mélange
![]() des états codés
des états codés ![]() affectés des probabilités
affectés des probabilités
![]() :
:
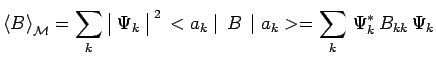 |
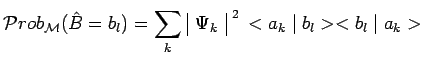 |
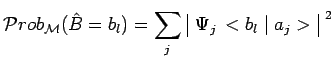 |
Ainsi, si la matrice ![]() n'est pas diagonale (c'est-à-dire si
n'est pas diagonale (c'est-à-dire si
![]() )
les expressions des deux valeurs moyennes sont différentes :
)
les expressions des deux valeurs moyennes sont différentes :
et les prévisions de mesure le sont également :
Si la mesure est effectuée sur l'état ![]() , l'expression de la
probabilité est le carré d'une somme cohérente de termes, dont la valeur
dépend de celles des phases relatives et dont le développement mélange les
contributions des différentes composantes de l'état
, l'expression de la
probabilité est le carré d'une somme cohérente de termes, dont la valeur
dépend de celles des phases relatives et dont le développement mélange les
contributions des différentes composantes de l'état ![]() .
.
Au contraire, si la mesure est effectuée sur un mélange
![]() ,
l'expression de cette probabilité est une somme des carrés des termes
précédents dont les contributions s'ajoutent alors d'une façon
incohérente, c'est-à-dire sans se mélanger et sans dépendre des valeurs des phases
relatives.
,
l'expression de cette probabilité est une somme des carrés des termes
précédents dont les contributions s'ajoutent alors d'une façon
incohérente, c'est-à-dire sans se mélanger et sans dépendre des valeurs des phases
relatives.