Un mélange quelconque de cas purs quelconques est toujours équivalent à un mélange de cas purs orthogonaux.
En effet, toute matrice ![]() est une matrice
semi-définie, c'est-à-dire que pour tout vecteur
est une matrice
semi-définie, c'est-à-dire que pour tout vecteur ![]() :
:
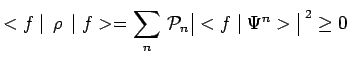 |
Puisque ![]() est hermitique, il existe une base
est hermitique, il existe une base
![]() qui diagonalise la matrice
qui diagonalise la matrice ![]() , et sur cette
base, les éléments diagonaux
, et sur cette
base, les éléments diagonaux
![]() ne peuvent être
négatifs puisque :
ne peuvent être
négatifs puisque :
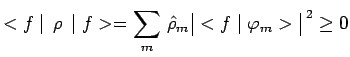 |
quel que soit ![]() , notamment
, notamment
![]() d'où
d'où
![]() sur la base qui
diagonalise la matrice
sur la base qui
diagonalise la matrice ![]() , l'opérateur
, l'opérateur ![]() prend sa forme
standard :
prend sa forme
standard :
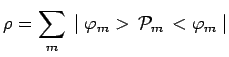 |
avec :
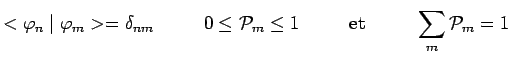 |
Question 2-7 : Démontrez que la matrice
![]() est également une
matrice semi-définie.
est également une
matrice semi-définie.