Pour bien comprendre tous les paradoxes que révèle la théorie quantique de la mesure, et qui seront exposés dans le chapitre V, il est important de démontrer ci-après l'impossibilité de représenter un cas pur sous la forme d'un mélange.
En effet, considérons le mélange ![]() de deux cas purs :
de deux cas purs :
que l'on peut écrire symboliquement :
Il en résulte successivement :
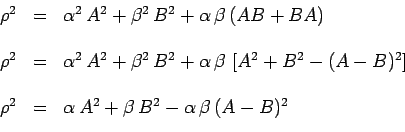 |
tenu compte de
![]() . On obtient donc :
. On obtient donc :
Pour que ![]() soit un cas pur, il faut :
soit un cas pur, il faut :
ce qui exige donc :
Or le carré de la matrice hermitique ![]() ne peut s'annuler que si cette
matrice est elle-même nulle. En effet :
ne peut s'annuler que si cette
matrice est elle-même nulle. En effet :
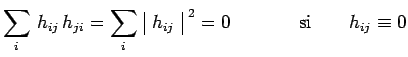 |
Si donc ![]() décrit un cas pur, le mélange considéré initialement avec
décrit un cas pur, le mélange considéré initialement avec
![]() n'était pas réellement un mélange. Inversement, si
n'était pas réellement un mélange. Inversement, si
![]() est bien un vrai mélange alors
est bien un vrai mélange alors
![]() et
et
![]() ne peut décrire un cas pur. En résumé, une combinaison linéaire
à coefficients positifs de cas purs (c'est-à-dire un mélange) ne peut jamais être
lui-même un cas pur.
ne peut décrire un cas pur. En résumé, une combinaison linéaire
à coefficients positifs de cas purs (c'est-à-dire un mélange) ne peut jamais être
lui-même un cas pur.
Question 2-8 : En choisissant pour base celle qui diagonalise la matrice
![]() , démontrez :
, démontrez :
Puisque la trace est invariante dans tous les changements de base, ces relations
sont bien caractéristiques. La valeur de
![]() est d'autant
plus faible que le mélange est important.
est d'autant
plus faible que le mélange est important.
Démontrez que l'équation
![]() constitue la condition nécessaire et
suffisante pour que
constitue la condition nécessaire et
suffisante pour que ![]() désigne un cas pur.
désigne un cas pur.