L'état intermédiaire est un cas pur

L'état ``$\alpha$ '' intermédiaire est alors représenté par un vecteur ket $\mid \alpha>$ , de telle sorte que :

$$\mathcal{P}rob\,(i\to \alpha\to f)=\begin{array}{\vert c\vert}<f\... ...}^{~2}=\begin{array}{\vert c\vert}<f\,\mid (\alpha)\mid \,i>\\ \end{array}^{~2}$$

L'amplitude globale de transition est donc factorisable :

$$<f\,\mid (\alpha)\mid \,i>=<f\,\mid \alpha>\,<\alpha\mid \,i>$$

Il y a lieu encore de déterminer ce vecteur $\mid \alpha>$ et pour cela il faut préciser si ce vecteur résulte d'une réduction du paquet d'ondes complète ou incomplète.

$\imath-$ Si cette réduction est complète, et la mesure peut alors être elle-même déclarée complète, l'état intermédiaire ``$\alpha$ '' est parfaitement caractérisé par le résultat de mesure obtenu, noté ci-après simplement $a$ . Ce résultat peut être, soit une valeur propre non dégénérée d'une seule observable $A$ ou un ensemble de valeurs propres d'un E.C.O.C. et le ket $\mid a>$ est le ket propre unique correspondant à ce résultat :

$$\hat{A}=a~~~\longrightarrow~~~a~~~\longrightarrow~~~\mid a>$$

L'amplitude globale de probabilité du processus complet est alors égale au produit des amplitudes séquentielles : $$<f\,\mid (a)\mid \,i>=<f\,\mid a>\,<a\mid \,i>$$ et la probabilité elle-même s'en déduit selon les formules générales précédentes.

$\imath\imath-$ Si cette réduction est incomplète, le ket $\mid \alpha>$ est encore un paquet d'ondes réduit et s'écrit :

$$\mid \alpha>=\frac{1}{N}\,\underset{a\in\mathbf{A}}{\sum\nolimits^\prime}\,\mid a><a\mid i>~~~~~~~~ \mathrm{avec}~~~<\alpha\mid \alpha>=1$$ la somme partielle $\Sigma^\prime$ portant sur tous les vecteurs propres orthonormés et associés à toutes les valeurs propres $a\,\in\,\mathbf{A}$ de $A$ non exclues par le résultat de cette mesureII17.

Le ket normé $\mid \alpha>$ peut encore s'écrire :

$$\mid \alpha>=\frac{P_\mathbf{A}}{<i\,\mid \,P_\mathbf{A}\,\mid \,... ...~~~ P_\mathbf{A}=\underset{a\in\mathbf{A}}{\sum\nolimits^\prime}\,\mid a><a\mid$$

d'où les expressions des amplitudes partielles :

$$<i\,\mid \alpha>=<i\,\mid \,P_\mathbf{A}\,\mid \,i>^\frac{1}{2}~~... ...\mid \,P_\mathbf{A}\,\mid \,i>}{<i\,\mid \,P_\mathbf{A}\,\mid \,i>^\frac{1}{2}}$$

et l'expression de l'amplitude globale :

$$<f\,\mid (\alpha)\mid \,i>=<f\,\mid \,P_\mathbf{A}\,\mid \,i>= \underset{a\in\mathbf{A}}{\sum\nolimits^\prime}\,<f\,\mid a><a\mid \,i>$$

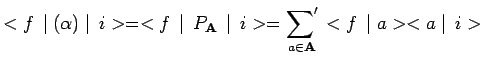et finalement celle de la probabilité :

$$\mathcal{P}rob\,(i\to\alpha\to f) = \begin{array}{\vert c\ver... ...\sum\nolimits^\prime}\,<f\,\mid (a)\mid \,i>\\ \end{array}^{~2}$$

L'expression de cette probabilité est le carré du module d'une somme de produits d'amplitudes séquentielles de probabilité.

Notamment, dans le cas où la mesure $\hat{A}$ porte sur une seule observable $A$ dont le spectre est discret et non dégénéré, $\mathbf{A}$ est le sous-ensemble des valeurs propres $a_k$ avec $k\,\in\,K^\prime$ non exclues par la mesure :

$$\mathcal{P}rob\,(i\to\alpha\to f) = \begin{array}{\vert c\ver... ...um\nolimits^\prime}\,<f\,\mid (a_k)\mid \,i>\\ \end{array}^{~2}$$

On remarque que la probabilité de transition $i\to f$ n'est pas égale à une somme de probabilités, c'est-à-dire à une somme de carrés de modules d'amplitude, mais qu'au contraire l'expression mathématique de cette probabilité est le carré du module d'une somme d'amplitudes partielles. On dit que, dans ce cas, la sommation est cohérente. Cette probabilité de transition : $$\mathcal{P}rob\,(i\to\alpha\to f) = \begin{array}{\vert c\ver... ...m\nolimits^\prime}\,<f\,\mid (a_k)\mid \,i>\\ \end{array}^{~2}+$$ $$\underset{l\not=m\,\in\,K^\prime}{\sum\nolimits^\prime} \,<f\,\mid (a_l)\mid \,i>\,<f\,\mid (a_m)\mid \,i>^*$$

n'est pas égale à la somme des probabilités associées à chacune des voies partielles ``$a_k$ '' avec $k\,\in\,K^\prime$ . Il s'y ajoute des termes croisés correspondants à $l\not=m$ et pour lesquels les contributions des voies partielles sont mélangées. Ce mélange est à l'origine du phénomène d'interférence entre ces voies partielles.

On remarque que les relations de phase entre les amplitudes partielles :

$$<f\,\mid (a_l)\mid \,i>~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{et}~~~~~~~~~~~~~~~~~~~~~~~~<f\,\mid (a_m)\mid \,i>$$

jouent un rôle capital dans le résultat final. En effet, multiplier chacune de ces amplitudes par un facteur de phase $e^{i\,\alpha_m}$ , arbitraire et différent, modifie complètement le deuxième terme du second membre.