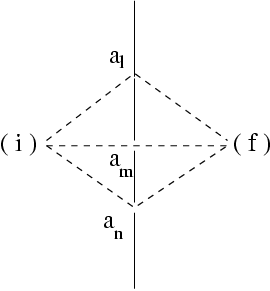
L'état intermédiaire est un mélange

L'état $\alpha$ intermédiaire est alors représenté par son opérateur densité $\rho$ . Cette situation est trivialement réalisée lorsque la mesure porte (éventuellement simultanément) sur un ensemble de systèmes identiques de même état initial ``$i$ '' et quand cette mesure est complète pour chacun d'entre eux, c'est-à-dire détermine son état intermédiaire représenté par l'un des vecteurs propres $\mid a_k>$ . C'est par exemple le cas de l'expérience des fentes de Young quand, pour chaque photon ou électron du faisceau incident, l'appareillage permet de déterminer quelle est la fente traversée. Dans ce cas, bien évidemment, les $N$ particules ou plus généralement les $N$ systèmes observés se trouvent distribués dans un ensemble quantique d'états effectivement occupés $\mid a_1>,\mid a_2>,\ldots$ etc.

Si $n_k$ est le nombre de systèmes placés dans l'état $\mid a_k>$ , on peut dire que chacun de ces $N$ systèmes se trouve distribué dans chacun de ces états et par exemple dans l'état $\mid a_k>$ avec une probabilité $\mathcal{P}_k$ mesurée expérimentalement et déterminée théoriquement :

$$\mathcal{P}_k=\lim_{N\to\infty}\,\frac{n_k}{N}=\begin{array}{\vert c\vert}<a_k\mid \,i>\\ \end{array}^{~2}$$

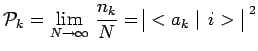L'état de ce système individuel, mais représentatif de l'ensemble, est alors représenté quantiquement par l'opérateur densité :

$$\rho=\sum\limits_k\,\mid a_k>\,\mathcal{P}_k\,<a_k\mid$$

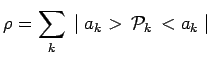Si la mesure constitue également un filtrage, c'est-à-dire élimine certains états, la somme ne porte plus que sur les états conservés avec $k\,\in\,K^\prime$ et l'opérateur doit alors être renormalisé de telle sorte que :

$$\rho^\prime=\frac{1}{N^2}\,\underset{k\,\in\,K^\prime}{\sum\nolim... ...~~~~\mathrm{avec}~~~~~~ N^2=\sum\limits_{k\,\in\,K^\prime}\,\mathcal{P}_k\leq 1$$

$$\mathrm{Tr}\,\rho^\prime=\frac{1}{N^2}\,\sum\limits_{K^\prime}\,\mathcal{P}_k=1$$

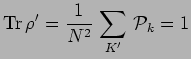La probabilité de transition de l'état initial dans l'état mélange est égale à sa probabilité de venir occuper chaque état ``$a_k$ '' où $k\,\in\,K^\prime$ avec la probabilité $\mathcal{P}_k$ :

$$\mathcal{P}rob\,(i\to\rho^\prime) = \sum\limits_{k\,\in\,K^\prime... ...ert c\vert}<a_k\mid \,i>\\ \end{array}^{~2}= <\,i\mid \,P_{K^\prime}\,\mid \,i>$$

$$\mathrm{avec}~~~~~~P_{K^\prime}=\sum\limits_{k\,\in\,K^\prime}\,\mid a_k><a_k\mid$$

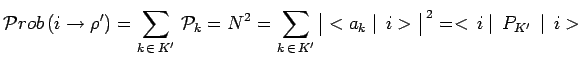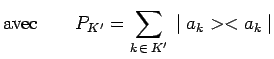Bien évidemment, si aucun filtrage n'est réalisé, la sommation $\Sigma^\prime$ porte sur toutes les valeurs propres $a_k$ et $P_K=1$ . La probabilité $(i\to\rho)$ est égale à 1. La mesure de $A$ a seulement transformé le cas pur $\mid \,i>$ en un mélange $\rho$ .

Enfin, la probabilité de transition de cet état mélange vers l'état final :

$$\mathcal{P}rob\,(\rho\to f)= \sum\limits_{k\,\in\,K^\prime}\,... ...ert}<a_k\mid \,f>\\ \end{array}^{~2}=<f\,\mid \,\rho\,\mid \,f>$$

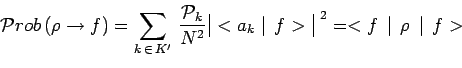n'est donc rien d'autre que la probabilité de trouver le mélange dans l'état $f$ .

La probabilité globale de transition $i\to(\rho^\prime)\to f$ est le produit des deux probabilités séquentielles précédentes :

$$\mathcal{P}rob\,(i\to(\rho^\prime)\to f)= \mathcal{P}rob\,(i\to\rho^\prime)\,.\,\mathcal{P}rob\,(\rho^\prime\to f)$$

$$\mathrm{soit}~~~~~~~~~\mathcal{P}rob\,(i\to(\rho^\prime)\to f)= <i\,\mid \,P_{K^\prime}\,\mid \,i>.<f\,\mid \,\rho^\prime\,\mid \,f>$$

auxquelles on peut associer deux amplitudes séquentielles :

$$A\,(i\to\rho^\prime)=<i\,\mid \,P_{K^\prime}\,\mid \,i>^{\frac{1}... ...} ~~~~~~~~A\,(\rho^\prime\to f)=<f\,\mid \,\rho^\prime\,\mid \,f>^{\frac{1}{2}}$$

Toutefois, il est remarquable que la présence de l'opérateur densité dans chacun des deux facteurs fait que le résultat final n'est pas factorisable :

$$\begin{array}{ccccl} \mathcal{P}rob\,(i\to(\rho^\prime)\to f)... ...vert}<f\,\mid (a_k)\mid \,i>\\ \end{array}^{~2} \\ \end{array}$$

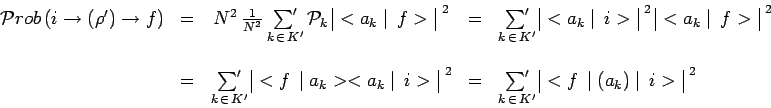La probabilité de transition globale est bien alors égale à la somme des probabilités partielles de transition avec passage par l'un des états intermédiaires $\mid a_k>$ avec $k\,\in\,K^\prime$ . On retrouve bien alors la loi classique d'addition des probabilités. Les voies partielles sont alors indépendantes et exclusives l'une de l'autre. Les phases relatives entre les amplitudes partielles $<f\,\mid (a_k)\mid \,i>$ peuvent être changées arbitrairement. Elles ne jouent plus aucun rôle. Les amplitudes partielles n'interfèrent plus entre elles. La probabilité globale de transition s'exprime comme une somme de termes au carré et non plus comme le carré d'une somme.